E.T. Jaynes 概率论：科学的逻辑 I [译]

这本书（可通过 这里 免费下载 PDF 版本）是理性思维领域的重要文献之一。Eliezer 曾将 Jaynes 称为 比我更高一层的思考者。我们认为 Jaynes 的论述十分清晰，这本书极具价值，但它更适合研究生物理学的读者。它填补了统计学、数学、因果理论和科学哲学之间的空白，提供了关于如何理解世界和面对不确定性的实际教训。在这里，我们试图提供一篇评论，分享书中的核心思想，并省略所有复杂的数学公式和推导过程。这本书大致由两部分组成：一半是高级数学，另一半是即便没有数学背景也能理解的精彩故事和见解。它包含丰富的内容，而这篇评论仅覆盖了前六章，介绍了概率论的基本概念和问题。

这本书分为两部分：

• 第一部分（第 1-10 章）：基本原理和初级应用
• 第二部分（第 11-22 章）：进阶应用

这是对第 1-6 章的评论

第一部分：概率论的新基础

书的前两章可能是最具挑战性的。在第一章中，Jaynes 用半章的篇幅回顾了形式逻辑，并将概率视为一种逻辑形式来介绍。其目标是将形式逻辑的规则扩展到概率推理上。这是一个不简单的任务，它试图将严格的二元真值观念转化为连续的概率观念，而不预设概率的任何定义。这也是本书名称的来源——科学的逻辑，因为正如 Eliezer 所说，Jaynes 认为在不确定性下进行推理是科学研究的基石。

第 1 章：合理推理

Jaynes 在本章的开头提出了这样一个情景：

想象在一个漆黑的夜晚，一位警察在街上巡逻，四周看似无人。突然，他听到了一个窃贼警报，望向街对面，发现一家珠宝店的玻璃窗被打破了。紧接着，一个戴着面具的男士从破碎的窗户爬出，手提一个装满昂贵珠宝的袋子。这位警察毫不犹豫地认定这个男士是个骗子。但他是如何通过推理得出这个结论的呢？让我们先来慢慢探索这类问题的本质。

在形式逻辑中，我们会遇到像“如果 A，则 B；A 成立，因此 B 也成立”这样的命题。这种逻辑被称为强三段式推理。下面是一个例子（假设在上，结论在下）：

IF Fisher dies before age 100, then he died a Frequentist
Fisher died at the age of 72
———————————————————————————————————
Fisher died a Frequentist

然而，对于 Jaynes 描述的窃贼案例，我们需要用到弱三段式推理。

Jaynes 试图将这种弱三段式推理形式化，他想象了构建一个机器人，这个机器人能够根据所收集的数据更新并输出某个结果的可能性。其具体实现取决于开发者，但必须满足三个基本条件，以便解决问题。这些条件是，值得注意的是，Jaynes 使用了“可能性”这个词，因为他还未正式定义“概率”这一概念，但我们可以将其理解为概率：

1. 可能性的程度用实数来表示。

2. 与常识有定性的一致性。

3. 一致性

   a. 如果可以通过多种方法推理出一个结论，那么所有可能的方法都应该得出相同的结果。

   b. 机器人应该考虑到它能接触到的所有相关证据，以解决任何特定的问题。

   c. 机器人应该用相同的可能性分配来表示相同的知识状态。

制造机器人的初衷在于，这是一种既客观又计算性的方法，它与包括弱三段论在内的人类直觉相兼容。

首个要求很好理解：即我们推导出的规则应当能按预期以数字形式排序。举例来说，如果 A 是 B 的证据，则表示“关于 B 的信息”的 $A\mid{}B$ 应大于单独的 $A$。第三个要求包含三个部分：3.a) 所有从证据到结论的路径应解析为相同的数值，意味着无论是知道某人有胡子和红色衣物，还是红色衣物和胡子，机器人最终的知识状态应该是相同的；3.b) 是一种贝叶斯方法，强调必须应用所有与问题相关的背景信息，例如我们预先知道开尔文温度不可能为负，因此应该为负温度分配零概率，尽管这会使计算变得复杂；3.c) 表示相同的概率应总是代表相同的确定性水平。

截至第 1 章，尚不明确这种机器人是否为最优选择，但其推理潜力似乎与人们的“常识”相符。

第 2 章：概率的基本定理

在第 1 章之后，我们可以进行逻辑陈述了。我们还有前一章中的三个基本需求，并留下了这样一个问题：我们的机器人还需要什么才能进行推理？结果只需要两样东西：乘积规则 (product rule) 和求和规则 (sum rule)。

本章可能是全书最枯燥的一章，因为它包含了推导概率论中链式规则和乘积规则所需的所有数学内容。虽然这可能有些乏味，但令人惊奇的是，Jaynes 在两章之后就建立了一个比科尔莫哥洛夫公理 (Kolmogorov axioms) 更为稳固的概率理论，而无需用到测度理论 (measure theory)。这是通过将逻辑陈述（如“鉴于 C，B 为真”）与两条我们在这里概述的规则联系起来实现的。

我们想要的是连接逻辑规则和数学函数的规则，这样我们就可以进行如下陈述：

Late fisher introduced fiduciary probabilities which are are inverse probabilities
Posteriors are inverse probabilities
——————————————————————————————————————————————————————————————————————
It is likely that Fisher would have eventually ended up a Bayesian.

乘积规则是我们需要的两条规则中的第一条。它是通过关注第三个基本需求 3a 来引入的。通过指出，首先接收信息 A，然后是信息 B，应该使我们处于与以相反顺序接收信息相同的知识状态：

我们首先寻找一个一致的规则，关联逻辑乘积 AB 的可能性与 A 和 B 分别的可能性。特别地，让我们探究 $AB\mid{}C$。考虑到推理的微妙性，我们将从几个不同的角度来分析这个问题。
作为初始方向，请注意，确定 AB 为真的过程可以分解为分别对 A 和 B 做出的基本判断。机器人可以：

1. 决定 B 为真；($B\mid{}C$)
2. 在接受 B 为真之后，决定 A 为真。$(A\mid{}BC)$ 同样地，
3. 决定 A 为真；$(A\mid{}C)$
4. 在接受 A 为真之后，决定 B 为真。$(B\mid{}AC)$

Jaynes 在他的论文中采用了 $A\mid{}C$ 的表达方式，而不是现代统计学中常见的 $p(A\mid{}C$)。这是因为在第二章，他正试图彻底重塑整个概率论和统计学，甚至包括基本的‘p’运算符。告诉你一个剧透：通过一系列复杂（对我们来说有些难以完全理解的）数学推导，他得出了经典的乘积法则：

$p(AB) = p(A\mid{}B)p(B) = p(B\mid{}A)p(A)$

而按照 Jaynes 自己的偏好，他更倾向于这种形式：

$p(AB\mid{}C) = p(A\mid{}BC)p(B\mid{}C) = p(B\mid{}AC)p(A\mid{}C)$

有意思的是，Jaynes 倾向于在公式中额外增加一个条件 $p(AB\mid{}C)$ 而不是简单的 $p(AB)$，来强调 $p(AB)$ 实际上是在已有的背景知识（先验知识）约束下的概率。在他看来，脱离任何信息背景的 $p(A)$ 概念是没有意义的。

而所谓的和规则，其实很简单：因为 A 和非 A 加起来总是等于 1（$A + \overline{A} = 1$），所以有

$p(A\mid{}B) + p(\overline{A}\mid{}B) = 1$

此外，这一章还提出了“无差别原则”。这个原则大致意味着，在没有任何先验信息的情况下，若有 N 种可能的结果，这些结果都同等可能。在这之前，Jaynes 一直用“可信度”来衡量各种结果的可能性。本章末尾，他引入了伯努利（1713 年）关于概率的原始定义，即从伯努利瓮中抽取球的过程，将其视为瓮中球数的比率。因此，概率在这里被定义为一个具体、便捷、标准化的量，与更广义的“可信度”概念相联系。

在这些规则和概率定义下，Jaynes 重新审视了机器人。这种机器人能接收信息，并根据这些信息输出不同结果的概率（而非可能性），以此来展示其客观性和决定性的特征。

“任何人只要掌握了相同的信息，却得出与我们机器人不同的结论，那么他们必然违反了某些基本原则。”

对于那些没有任何信息的情况，这点似乎是显而易见的（比如在伯努利罐案例中，为每个球被选中分配概率）。但对于那些无差别原则不适用的情况，这一点最初看起来有些问题（例如，你了解到其中一个球比另一个大两倍的边缘信息）。那些尝试遵循机器人规则的人可能会对这种情况下的每个球给出不同的具体概率值。但问题的关键已经不仅仅是球的大小，而更多地取决于个人对于球体尺寸如何增加被选中几率的看法。机器人的优点在于它要求明确地设定这些先验知识。理论上，如果两个人有相同的先验知识，他们就会得出相同的结论。当然，实际上我们很难为大多数问题详细列出所有先验知识，但这一原则仍然有助于我们理解如何为复杂问题推导出后验概率。值得一提的是，Jaynes 对“先验”这个概念的理解比多数贝叶斯统计学家和理性主义者要广泛得多。例如，我们在进行贝叶斯更新时使用的似然性或抽样函数，在 Jaynes 看来也是一种先验信息。从信息科学的角度看，Jaynes 的观点似乎是正确的；而从统计学的视角来看，这一点起初可能让人感到困惑，但它有助于我们更好地理解最大熵原理的概念。

第 2 部分：重新定义基础统计学

第 3 章：基本抽样理论

抽样理论构成了传统或频率统计学的根基。它专注于这样一种“前向概率”问题：如果一个罐子里有 5 个白球和 5 个红球，那么抽出两个白球的概率是多少。本章使用第 1 章和第 2 章的规则，重新推导了所有标准的类似硬币的分布。Jaynes 在这一章提出了两个引人深思的观点：

逻辑与偏好：

Jaynes 写这章时，人们对因果关系的理解远不如今天清晰。像 Penrose 这样的哲学家“认为现在时刻的概率只能依赖于之前发生的事件，而不能依赖于之后的事件”，因此，以下两种情况有着本质的不同：

• 我第一次从罐子里抽出一个红球；你认为第二个球是什么颜色？
• 我第二次从罐子里抽出一个红球；你认为第一个球是什么颜色？

但当我们将概率视为逻辑时，我们并不关心因果关系，而是关注手头的信息如何改变我们的看法。在上述案例中，无论是知道第一个还是第二个球是红色，都提供了关于罐子的同等信息，进而对未知抽取（无论何时发生）的推测也是相同的。在 Judea Pearl 的符号中，这种偏好与逻辑的区别通过引入一种新的表达方式得以解决，其中 $P(A\mid{}B)$ 表示 B 关于 A 的信息（如上所述），而新符号 $P(A\mid{}do(B))$ 则表示“实施 B”（而非仅仅知道 B）如何影响 A。

现实与模型之间的差异：

作为一名物理学家，Jaynes 更关注现实世界而不是数学模型中的理想化世界。如果你在一个真实的罐子中抽取球，那么球和罐子的大小和形状对推断过程有重要影响。那么，我们是否应该模拟球的物理属性呢？以下是 Jaynes 对这个问题的看法：

在概率论中，我们有一个非常巧妙的处理难题的方法：即便问题非常困难，我们还是能找到解决办法，具体步骤如下：

1. 让问题变得更加复杂；
2. 改变我们对“解决问题”的定义，使其成为我们能够做到的事；
3. 创造一个听起来非常专业和庄重的术语来形容这个过程，这样做在心理上有一种效果，就是隐藏了我们所做的真实行为，并让它看起来更加正当。

在替换抽样（sampling with replacement）的情况下，我们采用以下策略：

1. 比如说，在把球扔进瓮后，我们对瓮进行摇晃。这样一来，不管最初的问题有多么复杂，现在它变得更加复杂了，因为解决方案现在依赖于我们摇晃方式的每一个细节，除了前面提到的所有因素。
2. 然后，我们声称摇晃使得所有这些细节都变得不重要了，因此问题又回到了简单的伯努利瓮（Bernoulli urn）规则适用的情况。
3. 我们创造了一个听起来很庄重的词“随机化”（randomization）来描述我们所做的。这个词实际上是一种委婉说法，其真正含义是：当问题变得太复杂，我们无法处理时，故意抛弃相关信息。

我们用简洁的语言描述了这一过程，这是为了对抗一些概率论作者所营造的某种印象，他们将其神秘化了。对某些人而言，宣称问题是“随机化的”仿佛是行驱魔仪式般的咒语，目的和效果就像是清洗他们接下来的计算，使之免遭批判。我们这些怀疑论者常常羡慕那些坚定的信徒，他们似乎轻而易举地就获得了我们永远无法拥有的安全感。 … 单纯的摇晃并不能使结果变得“随机”，因为这个词在现实世界中基本没有意义；它在现实世界中没有一个清晰的定义。认为“随机性”是自然界中真实存在的某种属性，这是一种心理投射的谬误，其实质是“我不知道详细原因 - 所以 - 自然界也不知道。”摇晃所达成的效果截然不同。它不会以任何方式改变自然的运作；它只是确保没有人能对结果施加任何刻意的影响。因此，也就没有人能被指责操纵了结果。

第 4 章：基础假设检验

在前一章中，我们讨论了如何从假设 (H) 推导出数据 (D)，即 $P(D\mid{}H)$。但在实际情况中，我们经常先观察到数据，然后希望推断出这些数据背后的现象，也就是 $P(H\mid{}D)$。

这种逆向思维有时被称为“反向概率”，因为我们在条件概率中交换了 D 和 H 的位置。这也常被称为“假设检验”，目的是找出哪个假设最符合我们观察到的数据。

先验知识

为了实现这种逆向推理，我们需要依赖于所谓的“先验知识”。Jaynes 将机器人设想为始终掌握着某些信息 X，这些信息包括机器人自离开工厂以来所学习到的一切。因此，我们真正关注的不单是：

• $P(H\mid{}D)$：数据如何让我们相信假设 H，
• 而是 $P(H\mid{}XD)$：数据和我们的先验知识共同如何影响我们对假设 H 的看法。

只基于 X 的条件概率 $P(H\mid{}X)$ 被称为先验概率。需要明确的是，这里的“先验”是指在“信息/逻辑”层面上的先验，而非“时间/因果”层面的先验，因为信息理论中并不涉及时间变量。

先验信息指的是那些我们在数据变量中未包含的信息部分。在确定哪些是先验信息、哪些是数据时，有时会有一定的主观性。你当前的后验信息（基于已有数据得出的结论）将成为你下一个实验的先验信息。这个逻辑顺序同样适用于后验信息，它逻辑上在先验信息之后，但并非因果关系上的先后。例如，我可以推断，既然我今天检查时发现你的房子已经烧毁（先验），那么昨天你的房子可能也已经烧毁。在这里，信息的流向在因果关系上是相反的。

设定先验的四种常见方法包括：群体不变性、最大熵原理、边缘化和编码理论。本书主要关注前两种方法。

鉴于前三章已经介绍了逻辑、乘积与求和规则以及抽样理论，Jaynes 便轻松推导出了贝叶斯定理，并给予了我们熟知的表述：

通俗来说，这四个概率（或分布）被称为：

• $P(H\mid{}X)$ 是我们在获得数据之前对假设的先验信息
• $P(D\mid{}HX)$ 是似然函数或采样函数，说明在不同假设下数据的可能性，简单来说：假设对数据的解释是什么？
• $P(D\mid{}X)$ 是数据的概率，通常通过边缘化方法（遍历所有假设）计算得出
• $P(H\mid{}DX)$ 称为后验，包含了在考虑先验信息和数据之后我们获得的信息。

因此，当你阅读上述的贝叶斯定理时，可以这样理解：

需要注意的是，Jaynes 在他的书中将其表述为先验乘以似然，而不是像现代贝叶斯学派通常所说的似然乘以先验。

贝叶斯理论的实用更新

这本书中最简单的数学概念在第 4 章被引入。它本质上是贝叶斯定理的对数赔率形式，这种方法不仅酷炫，而且能快速计算，并有助于我们直观理解信念的更新过程，接下来我们将详细讨论。如果你对数学不感兴趣，可以直接跳到第 5 章。

首先，我们为假设 H 及其相反假设 $\overline{H}$ 写出后验概率公式：

$P(H\mid{}DX) = \frac{P(D\mid{}HX)P(H\mid{}X)}{P(D\mid{}X)}$

$P(\overline{H}\mid{}DX) = \frac{P(D\mid{}\overline{H}X)P(\overline{H}\mid{}X)}{P(D\mid{}X)}$

赔率和概率的关系可以理解为“发生”与“未发生”的比值。例如，如果某个事件发生的机会是 50/50，那么我们的赔率就是 1:1，或 $p/\overline{p}=0.5/0.5=1$；而对于 90% 与 10% 的情况，赔率则是 9:1，即 $0.9/0.1=9$。我们可以用同样的方法，通过相互除法计算上述两个后验公式的赔率。

$\frac{P(H\mid{}DX)}{P(\overline{H}\mid{}DX)} = \frac{\frac{P(D\mid{}HX)P(H\mid{}X)}{P(D\mid{}X)}}{\frac{P(D\mid{}\overline{H}X)P(\overline{H}\mid{}X)}{P(D\mid{}X)}}$

$O(H\mid{}DX) = O(H\mid{}X)\frac{P(D\mid{}HX)}{P(D\mid{}\overline{H}X)}$

这里的关键在于，两个方程都含有 $P(D\mid{}X)$ 这一项，而这恰是最难计算的部分。当我们对方程进行除法操作时，这个值就会被消除。因此，我们得到的结论是：后验概率（posterior odds）等于先验概率（prior odds）乘以在两种假设下数据的似然比（likelihood ratio）。

Jaynes 接着定义了一个名为“证据”（evidence）的函数，如下所示：

$e(H\mid{}DX) = 10\log\_{10}O(H\mid{}DX)$

这个证据函数被用于快速进行贝叶斯更新。就像 Eliezer 提出的 1 比特证据概念一样，这是从 1:1 赔率变为 1:2 赔率所需的证据量。Jaynes 使用分贝（decibel，dB）来作为他的证据尺度，类似于我们对声音的度量。在这种尺度下，0 dB 意味着 1:1 赔率，与 0 比特证据表示的 1:1 赔率相同，10 dB 代表 1:10 赔率，而 20 dB 则意味着 1:100 赔率（因为 10×10=100）。因此，每增加 10 dB 的证据，赔率提高 10 倍；而每增加 3 dB 的证据，则赔率提高约 2 倍（$10^.3$ 约为 1.99526）。换言之，13 dB 的证据相当于 1:20 的赔率。

我们可以使用这一方法来计算后验的证据量：

$e(H\mid{}DX) = 10\log\_{10}O(H\mid{}DX)$

$e(H\mid{}DX) = 10\log\_{10}\frac{P(H\mid{}DX)}{P(\overline{H}\mid{}DX)}$

现在，让我们来尝试理解这个公式。设想这样一个情境 $X$：有 11 个掠夺团队可能会攻击我们的城市，且总是由同一个团队对所有城市进行攻击。

• 其中 10 个团队由哥布林组成，他们攻破城墙的概率是 ⅙，
• 另外 1 个团队由更强大的兽人组成，攻破城墙的概率是 ⅓。

我们现在要考虑一个假设：我们是被兽人攻击的。根据先验情况，兽人攻击与否的比率为 10:1，因此 $e(H\mid{}X)=-10$。

为了弄清楚我们该如何根据新的数据（检查被攻击城市的城墙）来更新我们的判断，我们来看看所有可能发生的情况：

$P(\text{breached}\mid{}\text{orc},X) = \frac{1}{3}, P(\text{intact}\mid{}\text{orc},X) = \frac{2}{3}$

$P(\text{breached}\mid{}\text{goblin},X) = \frac{1}{6}, P(\text{intact}\mid{}\text{goblin},X) = \frac{5}{6}$

我们注意到城墙被破坏了，这意味着：

$10\log\_{10}(\frac{1/3}{1/6})=3~dB$

对数证据的有趣之处在于，无论是以分贝还是比特为单位，增加对数值就等同于乘以原始数值。由于多个事件的概率是所有单个事件概率的乘积，这相当于累加所有的证据。因此，我们可以直接把 3 加到初始的 -10 证据上，得出 -10+3=-7 的后验证据，说明是兽人所为。第二天，另一个城市遭到攻击，但城墙依然完好，这改变了证据：

$10\log\_{10}(\frac{2/3}{5/6})\approx{}-1\text{dB}|$

基于此，国王可以迅速审视所有遭受攻击的城市，计算城墙的状况，并得出以下结论：

$e(\text{orcs}\mid{}DX) = -10 + 3 \text{walls destroyed} - 1 \text {walls intact}$

在这个场景中，我们观察到 20 堵已经被摧毁的墙和 37 堵仍然完好的墙。这些观察结果给出了 $-10 + 3\times{}20 - 1\times{}37=13dB$ 的证据，支持兽人 (orc) 假说。换句话说，这意味着认为兽人是肇事者的可能性是不认为是兽人的可能性的 20 倍。

第 5 章：概率论的非传统应用

这是本书中引人入胜的一章。在书的后半部分，类似的章节比比皆是。Jaynes 通常会先打下坚实的统计学基础，然后再对频率主义者进行幽默而尖锐的批评。

在第 5 章，Jaynes 介绍了四个有趣的例子来展示概率论的实际应用，这些例子比传统的从瓮中抽球实验更具现实意义。这些例子被挑选出来是为了揭示一些违反直觉的观点和谬误。书中反复强调的一个主题是，在解读证据时，我们不应仅仅局限于考虑零假设（null hypothesis），因为这样可能导致错误的结论和不实的论证。同时考虑其他可能的假设也是非常重要的。

超感知力（ESP）

如果有人声称他们具有超感知力（ESP），并且能够反复准确地从 1 到 10 中猜出他人的数字，那么他们需要准确猜测多少次，才能让你相信他们真的拥有超自然能力？Jaynes 表示，即便是连续猜对 4 次，他也不会相信，但如果达到大约 10 次，他可能会开始考虑这种可能性。这意味着他最初对此持怀疑态度，信念强度可能低至 -40 dB，甚至可能是 -100 dB。在他引用的一个 ESP 实验中，声称拥有 ESP 能力的人在 37100 次尝试中猜对了 9410 次（占 25%），而纯粹依靠随机猜测的命中率为 20%。Jaynes 使用伯努利分布（Bernoulli distribution）的计算表明，这个结果仅凭偶然的概率极低，大约是 3.15e-139。

如果有人向你展示了一个实验结果，它与零假设的预期平均值相差 10 个标准差，因为样本数量（N）非常大，你是否就应该开始相信超感知力（ESP）呢？我们从 Less Wrong 这个思维训练网站学到的直觉是“当然不是”，这提示我们应该深入探讨问题，不仅仅局限于零假设。在像抽取瓮中球这样的理论问题上，你可能会接受这种做法，但在处理像超感知力（ESP）这样的实际问题时，你会用到一个基于终身经验构建的复杂世界模型，考虑许多其他可能的解释，并将这些证据与所有可能的解释进行对比。

如果我们仅考虑两种可能性：一是 ESP（特异功能）不存在，任何结果都是侥幸；另一则是某人真的具有 ESP，那么每次成功猜测就为 ESP 的存在提供了 +10 分贝（dB，声级单位）的证据。但是，Jaynes 表示：“事实上，即使他正确猜出了 1000 个数字，我仍不会相信他拥有 ESP”。这是因为在现实世界中，我们还需考虑许多其他假设，例如实验失误、错误的假定（如选择的分布并非均匀），以及欺诈行为，这些假设的先验概率虽然很低，但比 ESP 的概率要高，约为 -60 分贝。任何成功猜测都会使欺诈和实验失误的假设比 ESP 更有说服力，使其始终保持大约 40 分贝的优势。这意味着，Jaynes 需要其他类型的证据，而不仅仅是来自单一实验的反复正确猜测，才能使 ESP 假设显得足够合理。

乌鸦

Jaynes 接下来探讨的是直觉悖论，特别是在 Hempel 的悖论中提到的：“所有乌鸦都是黑色”。这个假设的证据是什么？一只黑乌鸦能证明这个假设吗？一只白色的鞋子又如何，因为从逻辑上说，“所有乌鸦都是黑色”等同于“所有非黑物体都不是乌鸦”，而白鞋正好是非黑非乌鸦的例证！通常，对什么构成证据的答案是“视情况而定”，但它不仅仅取决于“所有乌鸦都是黑色”的假设，还取决于我们考虑的其他替代假设。

I.J. Good 的回应（题为“白鞋是个误导”）展示了当你观察到一只黑色乌鸦，并只考虑两种假设时会发生什么：

• 一个世界里，乌鸦总是黑色但罕见（每 10000 只鸟中有 1 只是乌鸦，其余 9999 只是鹦鹉）；
• 另一个世界里，只存在乌鸦，但其中只有 10% 是黑色的。

如果这是你唯一的假设，那么看到一只黑乌鸦就相当于有 30 分贝 (即 1000:1 的比例) 的证据，支持你处于一个并非所有乌鸦都是黑色的世界。原因是在第一个世界中，每一只黑乌鸦在第二个世界中对应着 1000 只黑乌鸦和 10000 只白乌鸦，因此看到黑乌鸦更倾向于证明第二个世界的存在。

如果我们把第一个世界改为一个乌鸦永远是黑色并且非常普遍的世界，那么观察到黑乌鸦就更支持这个改变后的第一个世界，而非第二个世界。

这个故事直观地展示了 Jaynes 关于多假设的思想：一个数据点是否支持某个假设，取决于我们正在考虑哪些假设。这些故事的关键启示之一是，认识到不同假设的存在以及它们在我们心中的关系，是如何解读证据和分配概率的关键。理性主义者通常明白，一个事件的概率并不存储在被观察的物理对象本身，而是存在于观察者对该对象的不确定性中。在黑乌鸦悖论中，悖论感源于一种误解：认为概率存在于各个假设本身，而非所有假设相互关联及其与证据的关系中的不确定性。

人类是否使用贝叶斯推理？

Kahneman 和 Tversky (1972) 以及 Wason 和 Johnson Laird (1972) 的研究表明，人类在贝叶斯推理方面存在违反情况。其中最极端的例子是“如果 A，则 B”，许多人错误地将其等同于“如果 B，则 A”，其实正确的逻辑应该是“如果非 B，则非 A”。Jaynes 认为，这其实是贝叶斯推理的一种体现。例如，如果所有狗都是哺乳动物（逻辑推导），这也意味着某些哺乳动物是狗。具体来说，如果只有 20% 的动物是哺乳动物，这个信息就使狗的可能性增加了 5 倍！即 A 暗示 B 意味着 B 使 A 的可能性增加了 5 倍。

第 6 章：基本参数估计

在大多数统计学书籍中，这一章通常作为第一章或被认为是基础阅读。然而，现在我们已经来到了第 149 页，Jaynes 才首次引入参数这一概念。这就好比在编程的导论中写了 149 页却没有提及变量一词，理由是出于教学考虑。这种教学方法的目的是避免所谓的“心智投射谬误”。简而言之，如果你的模型（或计算机程序）设定了一个参数来描述从篮子中抽取红球的频率，那么这只是模型的设定，并不代表篮子本身的特性。你可能会问，怎么可能在不涉及任何变量的情况下写出 150 页的统计学内容？答案在于这些变量并非实际存在。Jaynes 的高明之处在于，他总是关注现实世界中的事件，而不是仅仅囿于他脑海中的统计模型参数。例如，他会讨论 $p(R\_3|R\_1,R\_2,X)$，即在前两次抽取红球的条件下，第三次抽出红球的概率，而不是讨论 $p(\theta|R\_1,R\_2,X)$，其中的 $\theta$ 代表瓮倾向于产生红球的性质。这正是 Jaynes 独到之处！

首先，我们来介绍最大似然估计，这是一种用来估算结果或参数的方法。当你能够为每一种可能的结果分配一个概率时，就可以应用这种方法，其核心是选择概率最高的结果作为估计。然而，这样做实际上会忽略许多关于数据分布的重要信息，有时候这些被忽视的信息其实非常关键。例如，在某些情况下，最大似然估计可能会给出与常理不符的预测（在信息论中称这些为“非典型”估计）。举个易懂的例子，如果你有一枚硬币，正面朝上的概率是 60%，反面是 40%，那么按照最大似然估计，连续投掷 1000 次硬币，最有可能的结果是 1000 次都是正面。注意，虽然这个全正面的结果在统计上最有可能，但它展示了最大似然估计的一些反直觉特性（比如，我们也可以用它来估计总共有多少次正面，而不是具体的投掷顺序，这样的话它会预测出大约 600 次正面）。在现实生活中，我们通常会期望看到一些反面，尤其当硬币越接近 50/50 时，反面的出现概率应该更高。但最大似然估计并不考虑硬币公平性的程度——只要硬币稍微有偏，无论如何它都会预测全是正面。进一步思考，我们会发现最大似然估计方法过于粗糙。实际上，由于物理上的细微差别，所有的硬币都可能稍微偏向某一面（比如正面的概率是 49.9999%，反面是 50.0001%），因此如果我们足够仔细，所有关于硬币投掷序列的最大似然估计都应该是全正面或全反面。这个例子说明了在已知硬币偏差参数的情况下，对结果进行最大似然估计的过程，这通常是更易于理解的情况。另一种应用是根据已有数据（如一系列硬币投掷）来找出最可能的参数估计值（例如硬币的偏差程度）。

Jaynes 针对物理学家的例子涉及一个放射性源发射粒子，以及一个能检测到部分粒子的传感器。这个放射性源平均每秒发射 $s$ 个粒子，这些粒子符合泊松分布（Poisson distribution），而传感器则以伯努利概率（Bernoulli rate）$\phi$ 来检测粒子。因此，如果 $\phi$ 是 0.1，长期来看，传感器能检测到大约 10% 的粒子。但如果你只有 $n=10$ 个粒子，就不能保证它会准确检测到 1 个粒子。同样，虽然我们可能每秒有 $s=100$ 个粒子，但任何给定的一秒钟都可能释放出多于或少于 100 个粒子。问题就出在这里。如果你使用最大似然估计（MLE），你每秒得到的粒子数总是 $\phi s$，因为 MLE“假定”每 10 个粒子中就有 1 个的关系是固定的，从而忽略了泊松分布源的变化性。例如，如果你有一个 $\phi = 0.1$ 的计数器，在某一秒钟观察到 15 个粒子，那么这一秒钟源头发出了多少粒子 $n$ 呢？按照 MLE，结果是 150 粒子。但 Jayne 的机器人给出的是 105 粒子。这个差异很大！这个例子也让实验物理学家们感到意外。之所以机器人给出 105 而不是 150，是因为放射源的变化性低于检测器，所以高读数并不一定是高于平均水平的粒子数的强证据。

虽然上述内容可能非常违反直觉，但通过绘制上面的分布可以解决所有混淆（尽管 Jaynes 并没有这样做）。下面是三张图表：

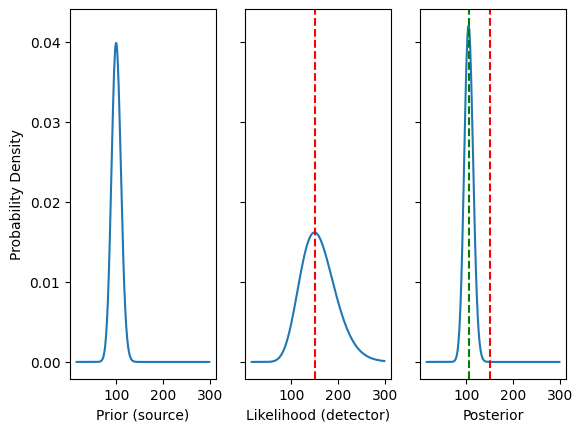
其中：

• 左侧是源，遵循泊松分布：$s \sim Poisson(k=100)$
• 中间是探测器，遵循二项分布：$n \sim Binomial(c=15, \phi=0.1)$
• 右侧是后验，是先验（源）和似然（探测器）之间的折中结果
• 红线代表的是最大似然估计值 150，绿线代表的是贝叶斯估计值 105。

不需要复杂的数学就能明白，先验是比较集中的，而似然则较为分散，因此后验的折中应该更倾向于先验。在现代术语中，这种方法被称为“全贝叶斯”，即利用完整的分布数据来进行推断，而最大似然估计方法则是希望通过分布的高峰部分来捕捉足够的信息。

回到数学的世界：通过运用泊松分布来模拟源强度和传感器计数所呈现的粒子分布，并利用整个后验分布来估算最初的粒子数量，Jaynes 的机器人将观察到的 15 个粒子视为可能的最小粒子数量（我们假设传感器不会在没有粒子的情况下产生计数），并在此基础上加上 $100(1 - 0.1) = 90$，其中的 100 来自于 $s$，0.1 来自于 $\phi$。正如硬币的例子所示，最大似然估计可能较为粗糙，因为它没有考虑所有的信息 — 在硬币的例子中，它忽略了偏置的程度。在这个粒子/传感器的例子中，最大似然估计没有考虑到源的强度，$s$。（我们应该指出，如果我们不提及通过提出不同的问题来改进最大似然估计的可能性，可能会过分贬低它，但关键在于，有时加入更多的信息是有益的，而最大似然估计往往会忽略这些信息）。作为非物理学家，我们也认为 Jaynes 可能在这里融入了一些物理学家固有的先验知识，比如如何看待粒子辐射的标准差。Jaynes 在他的论文中提供了更多细节：

“贝叶斯解法 (Bayes) 和最大似然解法 (maximum likelihood) 之间的差异何在？这种差异是由于我们拥有关于源强度 s 的先验信息。最大似然估计仅仅是在给定 n 粒子的情况下，最大化获得 c 计数的概率，得出的结果是 150。而在贝叶斯解法中，我们在最大化之前，会将这个概率乘以一个先验概率 $p(n|s)$，代表我们对之前情况的了解，由此得到一个完全不同的估计值。就像我们在第 6 章 '基本参数估计' 中所看到的，当反转葫芦分布时，简单的先验信息能显著改变我们对数据集的解读。”

Jaynes 用一种非常有趣的方式扩展了粒子传感器的例子：尽管关于传感器的信息相同，但由于先验信息（例如源是否被允许变化）的不同，得出了不同的结果。这充分展示了贝叶斯原理的实用性，即通过整合更多信息来获得更准确的估计，并接受估计之间的差异，作为信息差异的体现。

Jaynes 还提出了这个问题的更高级版本：人们进出一个含有未知强度源的放射性房间，每个人的放射性暴露都使用同一设备测量，该设备的 $\phi=0.1$。在这个例子中，第一个人测量到的计数对源强度的整体证据较弱，因此它为推断第二个人的暴露提供了相关信息。

个人观点

这本书只用 6 个章节就取得了令人赞叹的成就。Jaynes 从哲学角度出发，几乎只用逻辑和一些基本的愿望原则，就推导出了贝叶斯框架。相比之下，像 De Finetti 这样的其他贝叶斯学者通过赌博和漠然原则，更轻松地达到了许多相同的结论。Jaynes 个人对赌博作为统计学基础的看法颇为批判，认为太过粗俗。然而，真正的洞见并非源于他对逻辑的偏好，而是因为他的（贝叶斯）统计学建立在信息理论之上，而非赌博。在认识论上，探询“这些信息如何改变我的信念”要比探询“假如我是个赌徒，面对结果时应该怎样赌赔率，以避免被荷兰式赌局压倒？”更加直接明了。对于简单问题，Jaynes 和 De Finetti 会得出相同的先验和似然，但在复杂情况下，信息理论为设定先验提供了更好的出发点。

我们团队中有一员专注于蛋白质组学（研究身体内所有蛋白质的学科），他认为“在某些蛋白质中观察到性别的显著影响，因此其他蛋白质也很可能受到性别的显著影响”（这是信息理论的思考方式）。这种思考方式正是他在构建具有自适应先验的复杂分层模型时的思维逻辑。他并不会考虑“如果我是个赌博者，看到性别对某些蛋白质有显著影响，我就会使用这种特殊的自适应先验，以免在赌博中输给同事”。

这只是书的前四分之一内容的概述，其中许多细节被简化了。但书的核心精神和基础在这部分得到了很好的体现。其他章节涉及大量数学内容（如高斯分布的性质，以及 Jaynes 认为它应被称为中心分布的原因等），并深入探讨了数学和统计学的历史。正如我们蛋白质组学的例子所示，虽然这本书在每页的统计知识传授上并不多，但它却深刻地教会了我们如何思考统计学。正如书中的众多例子所示，统计和概率论中的直觉需要从常识出发，通过对信息和证据的细致思考逐步构建，否则我们可能会因自上而下的处理数据方法而错过底层信息的真正结构。

感谢 Mateusz Bagiński 和 LessWrong 的编辑们提供的宝贵反馈。