大语言模型的类比推理能力[译]

Michihiro Yasunaga,2,1 Xinyun Chen,1 Yujia Li,1 Panupong Pasupat,1 Jure Leskovec,2 Percy Liang,2 Ed H. Chi,1 Denny Zhou1 1 Google DeepMind 2 Stanford University

概要

“思维链”（CoT）提示法让语言模型在各类推理任务上表现优异，但是，这通常需要对推理过程的实例进行标记。在这个研究中，我们推出了一种新颖的提示（Prompting）技巧，名为“类推提示法（Analogical Prompting）”，旨在自动引领大语言模型进行推理。受到人类用过往经验解决新问题的类比推理方式启发，我们的方法激励语言模型在着手解决问题前，自主生成相关的实例或知识。这一策略有不少优势：它既不需要标记或寻找实例，通用且便利；同时能为不同问题定制生成的实例和知识，具有较强的适应性。实验数据显示，无论是在 GSM8K 和 MATH 的数学问题解答，Codeforces 的代码生成，还是 BIG-Bench 的其他推理任务中，我们的方法都比无示例（0-shot）CoT 和手动少示例（few-shot）CoT 表现更加出色。

1 引言

大语言模型（LLMs）在许多不同任务中都表现出色，比如 Brown 等人在 2020 年和其他研究团队在后续年份的研究都有展示（相关论文链接见上文）。近期，一种名为“链式思考（CoT）”的技术引起了人们的注意，它能让这些语言模型更好地处理复杂任务。通过 CoT 技术，我们可以引导模型生成一系列中间推理步骤来解决问题，如数学问题解决等。

以“少示例 CoT（few-shot CoT）”和“零示例 CoT（0-shot CoT）”为例，前者通过提供几个问题、理由和答案的示例来引导模型推理，后者则是通过提供“逐步思考”这样的指令来达到目的。这两种方法都在图 1 中有所展示。

然而，CoT 技术还有一些挑战需要克服。首先，我们需要提供相关的指导或推理示例来引导模型；其次，为减少手动标记的工作量，我们需要找到一种方法。例如，0-shot CoT 虽然提供了一般的推理指导，但对于一些复杂任务（比如代码生成）来说可能还不够。而 few-shot CoT 虽然提供了更详细的指导，但需要标记推理过程的示例，这会增加工作量和成本。因此，我们面临一个问题：能否有方法既能提供相关的指导或推理示例，又不需要手动标记呢？

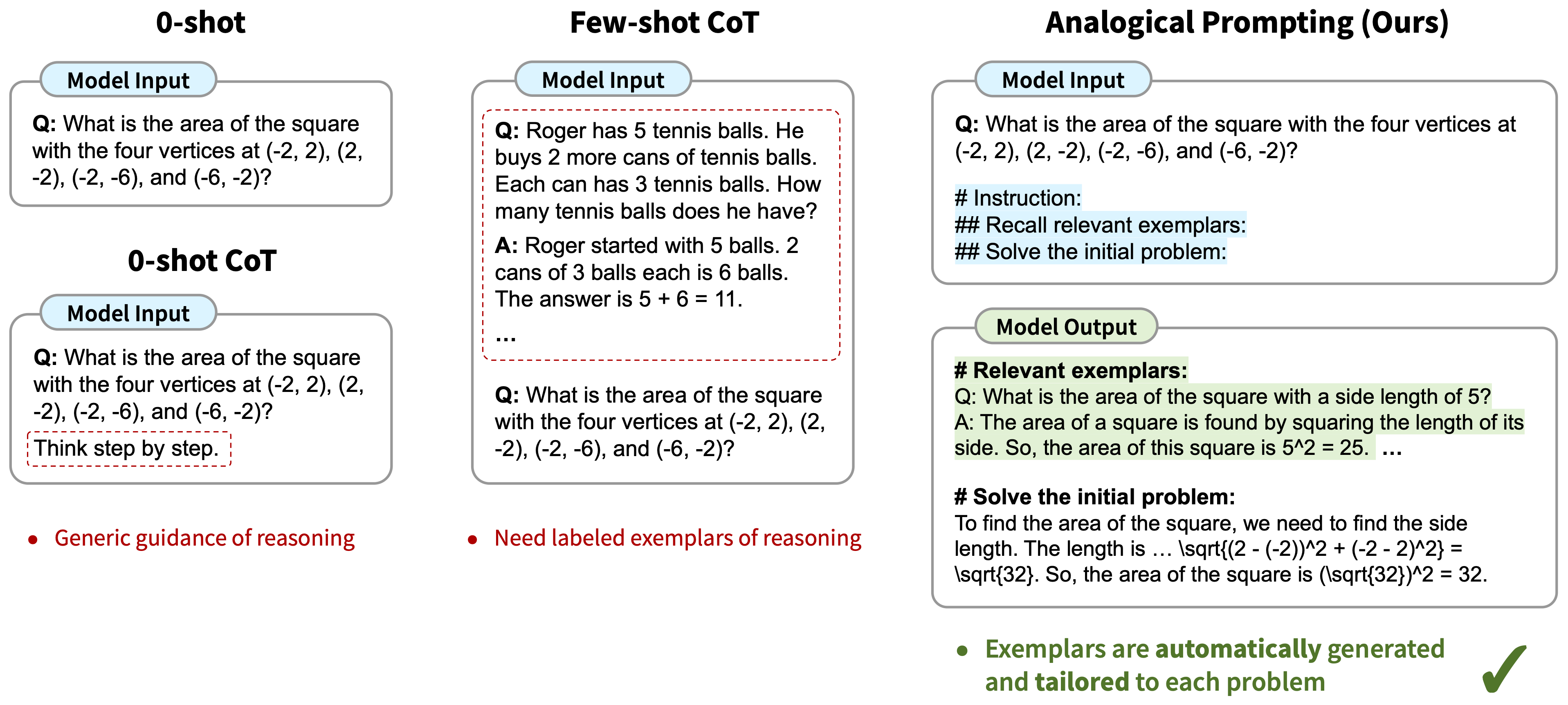
图 1: 我们的方法概览，类推提示法。左：在现有的方法中，要么是通用的（0-shot CoT），要么是需要标记示例（few-shot CoT）。右：而我们的方法是让模型针对具体问题自主生成相关的示例，这样就无需人工标记，同时还能为每个问题定制示例。更多细节可以参见图 3，其中模型自主生成了知识和示例。

在这个研究中，我们推出了一种名为 类推提示法（Analogical Prompting） 的新方法，通过它，大语言模型（LLMs）能更聪明地“思考”和解决问题。这个方法的设计灵感来源于人类的思考方式：当我们碰到一个新问题时（比如在坐标系中找出一个正方形的面积，参见图 1），通常会回想起以前是怎么解决类似问题的（比如计算已知边长的正方形的面积），然后运用到新问题上。此外，我们还会用到一些更抽象的知识，比如计算正方形面积需要知道它的边长。

如何操作呢？简单来说，给定一个问题，我们会引导 LLMs 用“#回忆相关的问题和解决方案：…”这样的指令，在上下文中“回忆”和生成相关的例子，然后基于这些例子去解决原始问题（参见图 1 和图 2）。同时，我们还可以让 LLMs 生成一些高层次的知识，以配合具体的例子，比如通过“#提供教程：…”这样的指令（参见图 3）。这在一些复杂的任务中特别有帮助，比如生成代码（详见第 6 章）。重点是，这个方法可以一次性生成知识、例子和解决方案。因为现代的 LLMs 在训练过程中已经“学会”了很多知识，我们只需通过提示让它们“回忆”和应用这些知识，就可以引导它们更好地解决新问题。

这个新方法有很多优点。首先，它能自动生成例子，这意味着我们不需要人工标记每个任务的推理例子，这解决了 0-shot 和 few-shot CoT 的挑战。而且，生成的例子是针对特定问题的，比如“几何”或“概率”，而不是笼统的“数学问题”，这简化了最近 CoT 技术的复杂性（参见 Zhang 等人，2022b 和 Shum 等人，2023）。

在多个需要推理的任务中，我们测试了这个新方法的效果，包括 GSM8K (Cobbe et al., 2021) 和 MATH (Hendrycks et al., 2021b) 中的数学问题，Codeforces 的代码生成任务，以及 BIG-Bench (Srivastava et al., 2022) 中的其他推理任务。我们使用了几个基础的 LLMs，比如 GPT-3.5，GPT-4 (OpenAI, 2023；Ouyang et al., 2022) 和 PaLM2 (Anil et al., 2023)。实验结果显示，这个新方法在不同的任务和基础 LLMs 上表现得都比 0-shot CoT 和 few-shot CoT 要好，平均准确率提高了 4%。尤其在涉及不同推理类型的任务上，如 MATH (包括代数，概率，几何等) 和 Codeforces (包括动态编程，图形算法等)，它表现得特别好。这说明，为每个问题生成定制的例子来引导 LLMs 的推理过程是行之有效的。

2 相关研究

2.1 大语言模型与引导技术

语言模型是计算文本可能性的智能系统。最近，科学家们成功地将这些系统从拥有数百万参数的模型（由 Devlin 等人在 2019 年研发）发展到有着数十亿参数的超级模型（由 Brown 等人在 2020 年提出）。并且，他们还在模型训练中加入了互联网上的文本和使用说明数据（参见 Gao 等人 2020 年，Ouyang 等人 2022 年，以及 Chung 等人 2022 年的研究）。这使得大语言模型在处理各种自然语言处理（NLP）任务上变得非常高效。

超大型 LLMs 凭借其数十亿的参数，展现出了出色的上下文学习和少样本学习能力（参见 Brown 等人 2020 年，Liu 等人 2022 年，Su 等人 2022 年，Mishra 等人 2022 年，Wei 等人 2022a 年，以及 Yasunaga 等人 2023 年的研究）。通过使用输入引导（可以是指令或一些示例数据），他们指导 LLMs 为特定任务生成期望的答案或反应。这标志着“引导技术时代”的开始。我们的研究方法正是利用了 LLMs 强大的上下文学习能力，通过自己生成的示例来引导模型进行推理。

有一项与我们的研究非常相近的工作是由 Sun 等人在 2022 年提出的“增强回忆生成”技术。在开放领域的问答（QA）任务中，这项技术能指导 LLMs 在回答问题之前先回忆相关的事实信息。而我们“自生成示例”的想法虽然与“回忆”有关，但我们更关注的是模型如何回忆和重现问题解决和推理的过程，而不仅仅是事实知识。

2.2“思路链”引导提示

“思路链”（Chain-of-thought，简称 CoT）由 Wei 等学者在 2022b 年提出，是一种独特的引导方式。它就像一个指路人，辅助大语言模型（LLMs）展现其解题过程中的每个思考步骤，帮助它更好地解决问题。其中，0-shot CoT 和 few-shot CoT 是两种常见的应用方式，分别由 Kojima 等人和 Wei 等人在 2022 年和 2022b 年提出。

0-shot CoT 是通过一个简单的指令，比如“一步一步地思考”，来激发 LLMs 的思维并展示其思考过程。而 few-shot CoT 则是通过提供一些例子，展示从问题到答案的完整推理过程，借助 LLMs 强大的学习能力，从而取得更好的效果。但是，这需要一些已经标记好的例子作为参考。为了解决这个问题，我们的方法是让 LLMs 自己创造例子。

在使用 few-shot CoT 的过程中，通常所有的测试问题都会使用一套固定的、已经标记好的例子。但最近有研究开始尝试使用基于检索的 CoT，也就是为每个具体问题从大量的外部数据中找到最相关的例子（参见 Zhang 等人 2022b 年和 Shum 等人 2023 年的研究）。与他们的研究目标相同，我们也是想提供相关的例子，但不是通过检索，而是让 LLMs 自己生成。这样不仅简单，因为不需要检索外部数据，而且更加灵活多变，LLMs 不仅可以创造特定的例子，还能够生成更广泛的知识和见解作为补充。实际测试表明，相比基于检索的 CoT，我们的生成型 CoT 在使用更大的基础 LLMs 时表现更好。

最后，还有一些其他的方法也可以提高 CoT 的效果，比如“自我一致性”（由 Wang 等人 2022 年提出）和“由简到繁”（由 Zhou 等人 2022 年提出）。这些方法可以和我们的研究相互补充，共同提高效果。

想了解更多相关的研究，请参考附录 A（§A）。

3 基础概念

我们正在研究如何解决问题的任务，就是说，针对一个给定的问题描述 $x$，我们要寻找解决方案 $y$，这可能是数学问题或编写代码的具体要求。这个解决方案不仅包括中间的思考过程或理由 $r$，还有最终的答案 $a$。

而“提示方法 $ϕ$”是一个可以把问题描述 $x$ 转换成 LLM（大语言模型）能理解的文本输入 $ϕ(x)$ 的功能，然后 LLM 会据此产生一个解决方案，表示为 $\hat{y} = \text{LLM}(ϕ(x))$。具体来说：

• 在“0-shot prompting”情况下，$ϕ$ 直接给出 $x$。
• 在“0-shot CoT”情况下，$ϕ$ 会在 $x$ 的基础上增加一些通用指示，比如“[$x$] 一步一步地思考”。
• 在“few-shot CoT”情况下，$ϕ$ 会在 $x$ 的基础上增加一些已经标记的例子 ${(x*i, r_i, a_i)}*{i=1}^{K}$，比如“[x1] [r1] [a1]...[xK] [rK] [aK] [x]”。

我们的最终目标是创造出一个新的“提示方法 $ϕ$”，可以提高 LLM 给出解决方案的准确度。

4 解决方案

我们推出了一种名为“类推提示法”的新方法，通过自动提供示例来指导大语言模型（LLM）的思考过程。就像人类在遇到新问题时会回忆起相关的过往经验一样，我们的方法使 LLM 在动手解决问题之前，能自动产生相关的示例或知识作为参考（详见图 1）。为了实现这一点，我们提出了两个技巧：一是自产生示例（详见 4.1），另一个是自产生知识 + 示例（详见 4.2）。

4.1 自产生示例

这个方法的核心理念是，现代 LLM 在训练过程中已经积累了丰富的解决问题的知识。通过明确指导 LLM 回忆或产生相关问题和答案，能帮助它们更好地学习和解决新问题。

比如，当我们有一个目标问题 x 需要解决时，我们可以给 LLM 下面这样的指令：

• # 问题：[$x$]
• # 相关问题：回想三个相关而独特的问题，并对每个问题及其解决方案进行描述。
• # 解决初始问题：

更多细节和实例，请参见图 2。首先，LLM 会产生几个（比如 K 个）与初始问题相关的示例，每个示例都包括问题、理由和答案（就是指令中“# 相关问题”部分）。然后，LLM 会利用这些示例来解决初始问题（“# 解决初始问题”部分）。值得注意的是，所有的指令都在一个提示中给出，让 LLM 可以一气呵成地产生相关问题和答案。而在指令中使用‘#’符号（比如‘# 相关问题’），能帮助 LLM 更清晰地组织回答。

以下是我们做出的几个关键技术选择：

• 产生相关和多样化的示例是很关键的：为了实现这一点，我们在指令中特意加入了如“创造出彼此有区别的题目”（参见图 2）的指示。这一步非常关键，因为有些 LLM 容易重复生成相同的题目，这在解题时可能会让人误解。

• 单次生成与独立生成示例的对比：有一种替代方案是独立地生成示例，通过分别从 LLM 中抽样，然后用所有示例重新提示 LLM。虽然这个方法也行得通，但我们目前采用的单次提示方式不仅性能可比，而且更为方便，无需多次提示。所以我们决定采用单次生成方式。

• 生成示例的数量（K）：经过实验，我们发现生成 3 到 5 个示例效果最佳（更多细节请参见 §6.5）。

我们的方法有两大优势。首先，它能提供详细的推理示例，无需人工标注，有效应对了 0-shot 和 few-shot CoT 的挑战。其次，这些生成的示例是为个别问题量身定做的（比如‘几何’或‘概率’），相比于传统 few-shot CoT 使用的固定示例（比如，通用数学问题；参见图 1），能提供更贴切的指导。

图 2：数学任务中，上方是我们提供的问题，下方则是 LLM，也就是 GPT3.5-turbo 给出的答案。我们在问题后附加了一些说明，让计算机能产生相关示例并解决这个问题。从下图可以看出，GPT3.5-turbo 所生成的示例与问题高度相关，且主要聚焦在概率学方面，并且成功、准确地解答了问题。更多详情，请参见 D.1 部分。

4.2“知识”与示例的双重生成

虽然产生示例是个好方法，但在一些复杂的任务，比如编写代码时，大语言模型（LLM）可能过分依赖这些基础示例，导致其在解决主要问题时无法有好的表现。为了解决这个问题，我们允许 LLM 自己生成一些高层次的要点来辅助示例，我们将其称为“知识”。举个例子，我们会在提示问题时加入额外的说明。具体的示例可以参见图 3。

• #教程：辨识问题的核心概念并提供相关教程。

另外，我们还发现，在生成示例前产生“知识”可以得到更好的结果（详情见表 6）。通过先产生“知识”，LLM 能更好地识别问题的核心概念，这也进一步帮助其产生更贴近问题核心，而非仅仅在表面层次上相似的示例。更多讨论，请参见 6.2 部分。

5 实验环境设置

图 3：这是我们为 Codeforces 任务设置的实验提示（上部）与 LLM 输出（下部）的真实示例。上图部分：我们的提示不仅包括了问题的描述，还附带有生成知识（比如，一些核心概念的教程）和相关示例的指导，最后再解决原问题。下图部分：GPT3.5-turbo 生成的知识和示例确实与要解决的问题紧密相关，主要集中在前缀乘积算法上。LLM 生成的最终代码则成功地运用了这一算法，有效解决了问题。更多细节和完整的提示与输出，请参见 §D.3。

5.1 实验任务

我们通过多个涉及推理的任务来评估我们提出的方法的有效性，这些任务包括解决数学问题、生成代码以及其他涉及逻辑和时间推理的任务。

解数学题

我们采用了一些广受欢迎的标准测试，比如 GSM8K（由 Cobbe 等人在 2021 年提出），这个测试包括了一些基础的数学题；还有 MATH（由 Hendrycks 等人在 2021b 年提出），包含了一些高中数学竞赛中的高难度数学题。我们针对每个问题使用温度设置为 0 的 LLMs 进行输出，并报告其准确性。

代码生成

代码生成是一种创造程序的过程，目的是解决算法问题。其中，竞赛编程是个挑战颇大的领域，它要求参与者能够熟练掌握和运用各种算法，比如动态规划和图算法 (Li et al., 2022; Kulal et al., 2019; Yasunaga & Liang, 2020)。

为了作为参考，我们从 codeforces.com 收集了一些竞赛编程题目（详细信息请参见 §B）。我们专注于 2023 年发布的 A 级题目，这样做是为了避免测试集的污染 (Magar & Schwartz, 2022)。每道题目都包含一个题目描述，这个描述会被输入到大语言模型（LLMs）中，然后通过一组测试用例来检验生成代码的正确性。只有代码能够通过所有的测试用例，我们才认为它是正确的。

我们的研究报告中采用了与早前的代码生成研究相一致的指标，即 Acc@1 和 Acc@10 (Li et al., 2022; Chen et al., 2023)。Acc@k 是用来衡量在 k 次模型输出样本中，至少有一次输出是正确的。我们从大语言模型中抽取 10 次输出样本来针对每个问题进行测试，并在抽样过程中设定温度为 0.7。

其他推理任务

我们还评估了 BIG-Bench (Srivastava et al., 2022; Suzgun et al., 2022) 中的多个推理任务，包括单词排序、五个对象的逻辑推理、时间序列推理、彩色对象推理以及形式谬误推理。这些任务形式各异，并可能没有相应的专用训练数据。因此，这些任务非常适合用我们的方法来生成定制的示例进行测试。对于每个任务，我们从大语言模型（LLMs）中得到输出，并且在输出温度设为 0 的条件下，记录模型的准确性。

5.2 选用模型

本实验选用了几款不同的基础大语言模型（LLM），包括 GPT-3.5-turbo、GPT-4（由 OpenAI 在 2023 年开发，2023，以及 Ouyang 等人在 2022 年的研究）（实验时间为 2023 年 6 月至 9 月），还有 PaLM 2-L（由 Anil 等人在 2023 年开发）。

5.3 比较的方法

我们比较了几种不同的指导方法，包括我们自己研发的方法。

0-shot 与 0-shot CoT

这些方法和我们的方法一样，都不依赖于带标签的样本。我们想要证明，我们的方法可以为大语言模型的推理过程提供更为精准的指导，从而获得更佳的执行任务的表现。

Few-shot CoT

标准的 Few-shot CoT 方法在同一数据集的所有测试问题中使用一组固定的推理样本。对于 GSM8K 和 MATH 数据集，由于它们的训练集中包含了标有推理步骤的解答，我们从这些训练集中选取了 K=5 个样本。对于其他数据集，我们手动注解 K=3 个样本。我们想通过实验展示，我们自行生成样本的方法，可以达到或者超过使用标签样本的基准线。

Few-shot retrieved CoT

这个方法不是使用固定的样本，而是针对每个测试问题动态地从训练集中检索相关的标有标签的问题和答案对。具体来说，我们使用 Sentence-BERT（由 Reimers 和 Gurevych 在 2019 年开发）对每个问题进行编码，然后根据余弦相似度从训练集中检索出最相似的 K=5 个问题。

我们的方法

在 GSM8K 数据集上，我们让模型自动生成 K=5 个样本；而在 MATH 和 BIG-Bench 任务上则生成 K=3 个样本。对于 Codeforces 任务，我们同时自动生成知识和 K=3 个样本。

6 结果简报

Prompting Methods	GSM8K Accuracy		MATH Accuracy
	GPT3.5-turbo	text-davinci-003	PaLM2	GPT3.5-turbo	PaLM2
0-shot	75.0%	14.8%	60.8%	33.0%	27.1%
0-shot CoT	75.8%	50.3%	78.2%	33.9%	29.8%
Few-shot CoT	76.7%	54.0%	80.7%	34.9%	34.3%
Ours: Self-generated Exemplars	77.8%	61.0%	81.7%	37.3%	34.8%

表 1: 展示了在 GSM8K 和 MATH 数学任务上，我们自主创新的提示方法（通过自行生成示例）表现突出，力压 0-shot CoT 和 few-shot CoT 等传统基准。对于 text-davinci 模型，我们使用了上下文示例来展示生成示例的方式。

Prompting Methods	GPT3.5-turbo-16k		GPT4
	Acc@1	Acc@10	Acc@1	Acc@10
0-shot	8%	24%	16%	30%
0-shot CoT	9%	27%	16%	29%
3-shot CoT	11%	27%	17%	31%
Ours: Self-generated Exemplars	13%	25%	17%	32%
Ours: Self-generated Knowledge + Exemplars	15%	29%	19%	37%

表 2: 在 Codeforces 代码生成任务上，我们的方法不仅胜过了 0-shot 和 few-shot CoT，自生成知识相较自生成示例还多了额外的优势，这在充满挑战的 Codeforces 任务中尤为显著。

Prompting Methods	Word sorting	Logical deduction five objects	Temporal sequences	Reasoning about colored objects	Formal fallacies
	0-shot	66.8%	30.0%	40.4%	50.4%	53.6%
0-shot CoT	67.6%	35.2%	44.8%	61.6%	55.6%
3-shot CoT	68.4%	36.4%	58.0%	62.0%	55.6%
Ours: Self-generated Exemplars	75.2%	41.6%	57.6%	68.0%	58.8%

表 3: 呈现了在 BIG-Bench 推理任务中的准确度表现，其中以 GPT3.5-turbo 作为基础大语言模型（LLM）。在多个不同的任务中，我们的方法不仅超越了基准（0-shot CoT），还能与 manual 3-shot CoT 媲美。

6.1 主要发现

解决数学问题

表 1 详细列出了 GSM8K 和 MATH 任务的表现。其中，我们通过自行生成示例的提示方法表现优异，轻松超越了 0-shot CoT 和 few-shot CoT 等。在 MATH 任务中，此方法在代数、概率和几何等不同推理类型的任务上表现尤为突出。这正验证了我们为每个问题量身定制示例的有效性。

图 1 和 2 以直观形式展示了 GPT3.5-turbo 利用我们的提示生成的输出例子。在这些例子中，LLM 成功产生了与问题相关的示例（如图 1 的几何问题和图 2 的概率问题），并据此给出了正确答案。然而，在常规的 few-shot CoT 情况下（见图 1），虽然示例与数学有关（如代数），但并不总是与实际问题（如几何）相匹配，这也反映了测试问题的多样性。

Prompting Method	(← scale down) text-curie-001	text-davinci-001	text-davinci-002	text-davinci-003 (scale up →)
0-shot	2%	6%	13%	14%
0-shot CoT	2%	6%	22%	50%
5-shot (fixed) CoT	2%	10%	43%	54%
5-shot retrieved CoT	3%	11%	47%	57%
Ours: Self-generated Exemplars	2%	9%	48%	61%

表 4：在 GSM8K 任务的测试中，我们可以看到性能的不同。随着基础 LLMs 的规模和强度逐渐增加（从左往右看），我们的新方法不仅超越了 0-shot CoT，还超过了使用固定示例的传统 few-shot CoT。有趣的是，在使用自创示例时，我们的方法与大型 LLMs 配合得更好，而对于小型 LLMs，使用检索出的示例的 few-shot CoT 表现更佳。

代码生成

表 2 揭示了 Codeforces 任务的成果。无论是在 GPT3.5-turbo 还是 GPT4 上，我们的引导方法都比如 0-shot CoT 和 few-shot CoT 这样的基准表现更出色。更进一步，自行生成的知识与自产生的示例相比，能够在处理棘手的 Codeforces 任务时提供更大的性能优势。利用我们的引导方法，GPT3.5-turbo 展现了与 GPT4 相媲美的表现，其中 GPT3.5-turbo 的 Acc@1 是 15%，GPT4 的 Acc@1 为 16%。

图 3（在 §D.3 有更详尽的版本）给出了一个定性的例子，展示了使用我们的引导方式生成的 GPT3.5-turbo 的输出。GPT3.5-turbo 生成的知识和示例与待解决的问题高度相关，并主要集中于前缀乘积算法。LLM 生成的最终代码成功地运用了此算法解决了问题。然而，在 0-shot CoT 的基准测试中，LLM 输出并未回顾相关示例，也未使用前缀乘积算法，导致了一个错误的解答方案 (§D.3)。

BIG-Bench 推理任务

表 3 呈现了 BIG-Bench 任务的成果。相较于 0-shot CoT 这样的基准，我们的引导方法表现更优，证明了其在多个任务中的有效性。此外，我们的方法还能与手动 few-shot CoT 相媲美。§D.4 为演绎推理任务（即“BIG-Bench 正式谬误”）展示了 GPT3.5-turbo 的输出实例。通过我们的引导方法，LLM 成功生成了相关的演绎推理示例。与此相反，0-shot CoT 在没有相关示例的情况下，往往会采用不正确的策略来处理演绎推理问题。

6.2 知识与示例相辅相成

在 Codeforces 任务（详见表 2）中，生成知识与示例是非常有益的，特别是当大语言模型（LLMs）需要用到复杂算法生成代码时。我们发现，知识生成有两大优势：一是它提供高层次的理解，补充示例的细节，防止 LLMs 过于依赖某个示例，更好地适应新问题；二是在生成知识时，LLMs 能够识别出问题的核心，产生与基本解决策略更一致的示例（如图 3 中的前缀产品算法），而不只是停留在字面上的相似性（如没有知识支持时，LLMs 产生的示例往往仅限于回文序列）。

然而，在其它任务，如 GSM8K 和 BIG-Bench 中，知识生成带来的性能提升并不明显，可能是因为这些任务相对简单。

6.3 自产示例与检索示例的比较

表 4：在 GSM8K 任务中的性能分析。我们的方法在所有大小的基础 LLMs 中都表现出色，比起 0-shot CoT 和有固定示例的 few-shot CoT 更优秀。如果是自产示例，我们的方法在大型 LLMs 中表现更佳，而检索得到的示例在小型 LLMs 中效果更好。

自产示例的主要优势在于它能提供解决问题的相关示例。另外，也可以从外部数据中检索相关示例，只要有一个标记了推理步骤的解决方案的示例数据集（比如 GSM8K 的训练集）。那么，这两种方式有哪些利弊呢？

检索法的明显优势在于其可靠性，因为从标签数据集中检索到的样例天然就是有效和正确的。与此相对，那些生成的样例则无法提供这样的保证。但检索通常需要有标签的样例，并包含一个复杂的附加检索步骤。

相对来说，生成法更简洁方便，不需要依赖外部的有标签数据或进行检索步骤。而且，生成法可以依据 LLM 接触过的所有（预）训练数据，创造出更适合特定测试问题的样例。然而，生成法也有其弊端：如果 LLM 不够强大或没有学习到与待解决问题相关的知识，它可能无法产生有效的样例。

表 4 列出了 GSM8K 任务的实验结果，对比了我们的自生成样例方法（“Ours”）和使用从 GSM8K 训练集检索样例的 CoT 方法（“5-shot retrieved CoT”）。实验涉及各种规模的基础 LLM，从 text-curie-001 到 text-davinci-003，其中“规模”概念上表示 LLM 所用的训练数据量和参数数量。

对于较大规模的 LLM（如 text-davinci-003），我们的方法优于检索的 CoT 方法。这可能是因为在训练过程中，LLM 有效学习了相关任务，从而可以生成有用的样例。然而，对于较小规模的 LLM，检索的 CoT 方法表现更佳，自生成法则未能产生有用或有效的样例。

6.4 基础语言模型的规模大小：模型越大，类推提示法的效果越好

表 4 展示了不同大小和能力的基础语言模型（从 text-curie-001 到 text-davinci-003）的表现，这些模型具有更多的参数和训练数据。我们的提示技巧在所有大小的模型上都比 0-shot 和 0-shot CoT 方法更好。当模型较小时（如 text-curie-001 和 text-davinci-001），使用带标签示例的 few-shot CoT 方法表现更优。但随着模型大小增加（如 text-davinci-002 和 text-davinci-003），我们的方法更胜一筹，这得益于模型能够更好地自主生成相关有用的示例。

6.5 示例生成数量的影响

Exemplars to self-generate	GSM8K	MATH
K=1	76.1	34.8
K=2	77.0	36.7
K=3	77.5	37.3
K=4	77.3	37.0
K=5	77.8	37.1

表 5：我们分析了生成示例数量（K 值）对我们方法表现的影响。使用 GPT3.5-turbo 作为基础模型，在 GSM8K 和 MATH 任务中进行测试。

表 5 中，我们探讨了在我们的方法中改变生成示例数量（K 值）的效果。当只生成一个示例（K=1）时，模型表现不佳，这是因为它过于依赖单一示例。当生成数量达到 3 或以上时，模型表现稳定，其中 K=3 或 5 时的表现最好。这个发现与 LLMs 在 few-shot 学习任务上的表现一致（参考 Brown 等人 2020 年的研究）。

我们在 GSM8K 和 MATH 中挑选了 50 个问题，研究了使用提示方法时产生错误答案的原因，并把这些错误归纳成了几种类型：

• （10/50）产生的示例与问题无关
• （12/50）虽然产生的示例与问题相关，但给出了错误的答案
• （28/50）示例与问题相关，答案也正确，但 LLM 却无法解决新的问题：
  • （12/50）示例和新问题之间的差异过大
  • （8/50）过分依赖某个示例，从而走错方向
  • （8/50）还有一些其他的问题，比如计算错误

大部分情况下，产生的示例还是与问题有一定的相关性，并且答案也是正确的。然而，常见的问题是，由于示例和新问题之间的差异，LLM 无法解决新问题（比如新问题的难度比示例要大）。这一发现促使我们在未来的研究中，不仅要生成与问题相关的示例，还要使这些示例有助于解决新问题的能力。

7 结论

---

我们引入了一种创新的语言模型提示技术：类推提示法。这一方法自行创造出相关的推理实例来协助问题解决，为每个独立问题提供详尽且定制化的示例，无需依赖标记过的数据。这种方式有效应对了目前 0-shot CoT 和 few-shot CoT 提示技术所面临的困境。实验结果证明，在包括数学题解、代码编写以及其他逻辑和时间推理任务在内的各种推理任务中，我们的方法表现优于 0-shot CoT 和 few-shot CoT。

方法的局限性及未来研究方向

我们的技术存在一定的局限。首先，与普通的 0-shot 和 0-shot CoT 相比，我们的技术增加了推理计算量，因为它产生了更多的令牌。而与 few-shot CoT 相比，虽然输入令牌较少，但输出令牌较多，因为在 few-shot CoT 中，示例被视为输入，而在我们的技术中，示例被计为输出。此外，如果 LLM 不够强大或未学习到解决新问题所需的相关知识，自生成过程可能会失败。但若 LLM 更为强大，就能借助先前的相关知识处理更为复杂的问题，所以我们的方法更适用于较强大或大规模的 LLMs。最后，据 Jiang 等人在 2020 年的研究，LLM 的表现会受到用于询问模型的特定提示语的影响，我们的研究同样存在这一敏感性问题。

鸣谢

感谢 Google DeepMind、Stanford SNAP 和 P-Lambda 团队的 Qian Huang、Chen Liang、Andrew Dai 及其他同事对本研究的宝贵意见和建议。

附录

附录 A：额外的相关研究

a.1 语言模型与推理技巧

推理，简而言之，就是运用所学知识去解决新问题，通常这个过程需要多个步骤。而让计算机语言模型具备推理能力，已经是学术界探索多年的课题了，这方面有很多值得一读的研究（比如 Bottou 在 2014 年的研究，还有 Zhao 等人在 2023 年，以及 Wei 等人在 2022 年的研究）。

为了能准确地衡量这些语言模型在推理方面的表现，研究者们专门设计了一些数据集，用来测试模型在不同需要推理的任务上的表现，比如多步骤的问题回答，数学题解答，以及编写代码等等。我们的研究就是基于这些多样化的数据集来进行的。

研究者们为了让语言模型更好地“推理”，采用了许多不同的方法，比如在训练过程中使用更多需要推理的数据，检索结构化知识，甚至加入了外部的推理模块，比如逻辑运算和程序执行等。

近年来，随着大语言模型（LLMs）的出现，通过设置不同的提示让它们进行推理，这个方法已经被证明是有效的，并且越来越受到大家的关注。比如有一种常见的做法是让 LLMs 生成推理过程中的中间步骤，就像 chain-of-thought 方法那样，可以帮助 LLMs 更好地完成复杂的推理任务。还有很多其他研究也在这个方向上做了很多有意义的工作，他们通过使用更多结构化的算法和搜索方法，甚至长期的行动和计划，以及将不同的工具和程序集成到推理过程中来。

我们的工作就是在这些研究的基础上，为了增强 LLM 的推理能力做出的一点微小的贡献，而且这还是第一次尝试从人类的类比推理中获取灵感，来改善 LLM 的推理过程。

a.2 类比推理：思维的捷径

当我们遇到新问题时，经常会不自觉地回想过去的经验来寻找答案，这就是所谓的“类比推理” (Gentner & Holyoak, 1997)。这个现象在心理学领域被深入研究，显示它在解决问题 (Gentner & Markman, 1997) 和激发创造力 (Ward et al., 1997) 等多种思维活动中都发挥着关键作用。简单来说，类比推理就是通过找到过去和现在情境之间的共同点，帮助我们更轻松地转移和应用知识 (Dunbar, 2001)。

类比推理不仅影响着我们人类的思维方式，还在人工智能和机器学习的发展中起着推动作用 (Carbonell, 1983; Mitchell et al., 1986)，被用作一种评判标准，检验机器学习模型的推理能力 (Bian et al., 2014; Huang et al., 2021)。

我们的研究是首次尝试利用类比推理的原则来优化语言模型推理过程的突破性工作。

附录 B：Codeforces 数据收集简介

按照早前研究的步骤 (Li et al., 2022; Kulal et al., 2019; Yasunaga & Liang, 2021)，我们从 codeforces.com 收集了一批数据。我们选取了 2023 年 1 月至 8 月期间发布的 Level-A 难度的问题。这些问题包含完整的问题描述和测试用例，都可以在网站上找到。其中，有些测试用例因为长度过长被截断，我们没有采用。最终，我们选取了长度在 GPT3.5-turbo 可处理的 2000 令牌内的问题，共计 50 个。由于数据集规模相对较小，我们进行了两轮评估，并最终报告了平均结果。

附录 C：其它研究成果

Prompting Method	Acc@1	Acc@10
Ours: Self-generate knowledge after exemplars	14%	27%
Ours: Self-generate knowledge before exemplars	15%	29%

表 6: 展示了使用 GPT3.5-turbo 在 Codeforces 任务上进行的消融学习实验结果。相比之下，在生成样例之前就进行自我生成知识的方法略微优于在生成样例之后进行的方法（详见 4.2 节)。

附录 D：完整示例

D.1 数学部分

我们的提示词（自动生成示例）：

你的任务是解数学题。当遇到一道数学题时，请你先回想一些相关的题目作为例子。然后，再去解决最开始的那个问题。

# 最开始的问题：

有一家航空公司为飞机上的每位乘客提供晚餐，乘客可以选择牛排或者鱼。六名机组人员中有三人可以选择牛排，三人可以选择鱼。如果食物是随机分配的，那么两名飞行员都拿到鱼的概率是多少呢？

# 操作指南：

你的答案中必须包含以下几点：

## 相关问题：

请你想出三个和最开始的问题相关的数学问题作为例子。注意，每个问题都应该和其它问题有所区别，包括和最开始的问题（比如，涉及不同的数字和名字）。每个问题都要按照以下的格式：

- “Q：”后面写问题描述

- “A：”后面写问题的解决方法，并把最终答案写在 \boxed 里。

## 解决最开始的问题：

说：“我们来解决下面这道数学题。”然后按照以下的格式回答：

Q：把最开始的问题复制粘贴在这里。

A：解释解决方案，并把最终答案写在 \boxed 里。

GPT3.5-turbo 输出结果：

类似问题：

问：有个袋子里面装了 5 个红球和 3 个蓝球，如果从中不放回地随机抽两个球，那么两个球都是红的概率是多少呢？

答：袋子里总共有 8 个球。首次抽球时，拿到红球的概率是 5/8。拿到一个红球以后，袋子里还剩 4 个红球和 3 个蓝球，此时再拿到红球的概率就是 4/7 了。要计算的两次都拿到红球的概率，只需要把两次抽球的概率相乘：$(5/8) \times (4/7) = \boxed{\frac{5}{14}}$。

问：假如有个盒子，里面有 10 个红色弹子和 5 个蓝色弹子。如果不放回地抽三个弹子，那么全部抽到红弹子的概率是多少？

答：这个盒子里总共有 15 个弹子。首次抽到红弹子的概率是 10/15，也就是 2/3。抽出一个红弹子后，盒子里剩下 9 个红弹子，14 个弹子总计。第二次抽到红弹子的概率是 9/14。再抽出一个红弹子，盒子里就剩下 8 个红弹子，13 个弹子总计了。此时，第三次抽到红弹子的概率是 8/13。我们只需把每次抽到红弹子的概率相乘，就得到了抽三个红弹子的概率：$(10/15) \times (9/14) \times (8/13) = \boxed{\frac{24}{91}}$。

问：一个袋子里有 4 个绿色弹子、3 个红色弹子和 2 个蓝色弹子。如果我们不放回地从中抽两个弹子，那么抽到的两个弹子都是绿色的概率是多少？

答：袋子里总共有 9 个弹子。第一次抽到绿色弹子的概率是 4/9。然后袋子里就剩下 3 个绿色弹子和 5 个非绿色弹子了，所以第二次再抽到绿色弹子的概率是 3/8。两次抽到绿色弹子的概率就是两者的乘积：$(4/9) \times (3/8) = \boxed{\frac{1}{6}}$。

再来看一个实际问题：

有个航空公司给飞机上的所有乘客提供晚餐，乘客可以选择牛排或者鱼。飞机的 6 名机组成员可以从三份牛排和三份鱼中选择。如果给机组人员的餐食是随机分配的，那么两个飞行员都选择了鱼的概率是多少？

答：一共有 6 名机组人员，首个飞行员拿到鱼的概率是 1/2。当首个飞行员拿到一份鱼后，剩下的是两份鱼和三份牛排，所以第二个飞行员拿到鱼的概率是 2/5。两个飞行员都拿到鱼的概率就是这两个概率的乘积：$(3/6) \times (2/5) = \boxed{\frac{1}{5}}$。

D.2 GSM8K

我们的任务提示词（自行生成的示例）:

你需要解决数学问题。遇到数学题时，想想与之相关或相似的题目作为例子，然后再去解决最开始的那个问题。

# 初始问题：

Kyle 用 $19.50 的价格购买了去年最畅销的书，这个价格是打了 75% 的价格。那么，这本书的原价是多少？

# 注意事项：

请确保你的回答遵守以下的说明。

## 类似问题：

请给出五个与初始问题相关或相似的数学问题的例子。对于每个问题，详细地说明解决的步骤，并给出最后的答案（请用 \boxed 括起来）。对于每个问题：

- 在“Q: ”后面写出问题。

- 在“A: ”后面解释解决方案，并在 \boxed 中写出最终答案。

## 解决初始问题：

Q: 在此处复制并粘贴初始问题。

A: 解释解决方案，并在 \boxed 中写出最终答案。

GPT3.5-turbo 输出结果：

类似问题：

Q1：一件原价 $40 的衬衫现在打八折，销售价是多少？ 答：衬衫原价 $40，八折之后，可以节省 $40 的 20%，即节省了 $8。所以，衬衫的销售价是 $40 减去 $8，等于 $32。

Q2：商店所有商品都有 15% 的折扣。一个顾客用 $85 买了双鞋，那么鞋的原价是多少呢？ 答：设鞋的原价为 $x。15% 的折扣意味着可以省下 $x 的 15%，即省下 $0.15x。已知销售价为 $85，我们可以建立方程 $x - $0.15x = $85，进一步计算可得鞋的原价是 $100。

Q3：餐厅对所有餐品提供 10% 的折扣。顾客付了 $45 的餐费，那么原价是多少？ 答：设餐品原价为 $x。10% 的折扣相当于省下 $x 的 10%，也就是 $0.10x。已知销售价是 $45，可以建立方程 $x - $0.10x = $45，从中我们得知餐品原价为 $50。

Q4：一台原价 $800 的笔记本现在打七折，销售价是多少？ 答：笔记本原价 $800，打七折后，折扣金额是 $800 的 30%，即 $240。所以，打折后的价格是 $800 减去 $240，等于 $560。

Q5：商店所有玩具打 12% 的折扣。顾客用 $22 买了个玩具，那么玩具的原价是多少？ 答：设玩具原价为 $x。12% 的折扣就是省下 $x 的 12%，即 $0.12x。销售价为 $22，通过方程 $x - $0.12x = $22，我们算出玩具原价为 $25。

最初的问题解答：

Q：Kyle 花了 $19.50 买了去年最热卖的书，这个价格是原价的 75%。那么这本书的原价是多少呢？ 答：设书的原价为 $x。25% 的折扣意味着省下 $x 的 25%，也就是 $0.25x。已知销售价为 $19.50，通过方程 $x - $0.25x = $19.50，我们算出书的原价是 $26。

D.3 Codeforces

Our prompt (self-generate exemplars and knowledge):

Your goal is to write Python3 code to solve competitive programming problems. Given a problem, explain the core concepts in it and provide other relevant problems. Then solve the original problem.

# Problem:

You are given a sequence a_1, a_2, \\ldots, a_n. Each element of a is 1 or 2. Find out if an integer k exists so that the following conditions are met.

1 \\leq k \\leq n\-1, and a_1 \\cdot a_2 \\cdot \\ldots \\cdot a_k \= a\_\{k+1\} \\cdot a\_\{k+2\} \\cdot \\ldots \\cdot a_n, where \\cdot denotes a product.

If there exist multiple k that satisfy the given condition, print the smallest.

Input

Each test contains multiple test cases. The first line contains the number of test cases t (1 \\le t \\le 100). Description of the test cases follows.

The first line of each test case contains one integer n (2 \\leq n \\leq 1000).

The second line of each test case contains n integers a_1, a_2, \\ldots, a_n (1 \\leq a_i \\leq 2).

Output

For each test case, if there is no such k, print \-1.

Otherwise, print the smallest possible k.

# Instruction:

## Algorithms:

Identify the core concepts or algorithms used to solve the problem.

## Tutorial:

Write a useful tutorial about these algorithms.

## Example Problems:

Provide three examples of relevant competitive programming problems that involve these algorithms. For each problem, describe the problem, explain the solution in detail, and then write the correct Python3 code.

## Python3 code to solve the original problem:

Include the following points in your response:

\- Explanation of the solution:

\- Python3 code to solve the problem:

Output by GPT3.5-turbo-16k:

## Algorithms:

The core algorithm for solving this problem is the prefix product algorithm.

## Tutorial:

The prefix product algorithm is used to calculate the product of all the elements in a prefix of an array. It is a useful algorithm for solving problems that involve calculating the product of all the elements in a subarray.

The algorithm works by initializing a variable "prefix" to 1, and then iterating through the array from left to right. At each iteration, the current element is multiplied with the prefix, and the result is stored in the prefix variable. This way, the prefix variable keeps track of the product of all the elements in the prefix of the array.

Here is the pseudocode for the prefix product algorithm:

The time complexity of this algorithm is O(n), where n is the size of the input array.

## Example Problems:

1. Problem: Given an array of integers, find the product of all the elements in each subarray of size k.

   Solution: We can use the prefix product algorithm to solve this problem. We initialize a prefix variable to 1, and then iterate through the array from left to right. At each iteration, we multiply the current element with the prefix, and store the result in the prefix variable. If the index i is greater than or equal to k\-1, we divide the prefix by the element arr\[i\-k+1\], which represents the first element of the subarray of size k starting at index i\-k+1. The result is the product of all the elements in the subarray of size k starting at index i\-k+1. We can store these results in a new array and return it as the output.

2. Problem: Given an array of integers, find the longest subarray with a product less than or equal to a given target.

   Solution: We can use the prefix product algorithm to solve this problem. We initialize a prefix variable to 1, and then iterate through the array from left to right. At each iteration, we multiply the current element with the prefix, and store the result in the prefix variable. If the prefix becomes greater than the target, we divide the prefix by the first element of the subarray, and move the start pointer of the subarray one step forward. We update the maximum length of the subarray if necessary.

3. Problem: Given an array of integers, find the smallest k such that the product of all the elements in the prefix of the array is equal to the product of all the elements in the suffix of the array.

   Solution: We can use the prefix product algorithm to solve this problem. We initialize a prefix variable to 1, and then iterate through the array from left to right. At each iteration, we multiply the current element with the prefix, and store the result in the prefix variable. We also initialize a suffix variable to 1, and then iterate through the array from right to left. At each iteration, we multiply the current element with the suffix, and store the result in the suffix variable. If the prefix is equal to the suffix, we return the current index as the smallest k. If no such index is found, we return \-1.

Below is a baseline output generated by GPT3.5-turbo-16k using vanilla 0-shot prompt. This output does not recall any relevant exemplars and fails to employ the prefix product algorithm, resulting in an incorrect solution.

D.4 BIG-Bench: formal fallacies

Our prompt (self-generate exemplars):

Your task is to tackle reasoning problems. When presented with a problem, recall relevant problems as examples. Afterward, proceed to solve the initial problem.

# Initial Problem:

"Is Siri a stepsister of Mary? Is Susan related to Kate? In large families, it is sometimes difficult to keep track of all one’s relatives. The following argument seeks to clarify some such relations: To start with, everyone who is a schoolmate of Mildred is a daughter of Jeanette, too. Now, being a daughter of Jeanette is sufficient for not being a cousin of Cristi. Therefore, no schoolmate of Mildred is a cousin of Cristi." Is the argument, given the explicitly stated premises, deductively valid or invalid? Options: \- valid \- invalid

# Instructions:

Make sure to include all of the following points:

## Relevant Problems:

Recall three examples of problems that are relevant to the initial problem. Note that your problems must be distinct from each other and from the initial problem. For each problem:

\- After "Q: ", describe the problem

\- After "A: ", explain the solution and enclose the ultimate answer in \\boxed\{\}.

## Solve the Initial Problem:

Say "Let’s solve the following reasoning problem." Then formulate your response in the following format:

Q: Copy and paste the initial problem here.

A: Explain the solution and enclose the ultimate answer in \\boxed\{\} here.

Output by GPT3.5-turbo:

Relevant Problems:

Q: In a certain town, all doctors are required to have a medical degree. John is a doctor. Therefore, John must have a medical degree. Is this argument valid or invalid?

A: This argument is valid because it follows the logical form of a categorical syllogism, where the first premise establishes a universal statement and the second premise applies that statement to a specific case. Therefore, the conclusion can be logically deduced. \\boxed\{valid\}

Q: All cats have fur. Fluffy is a cat. Therefore, Fluffy has fur. Is this argument valid or invalid?

A: This argument is valid because it follows the logical form of a categorical syllogism, where the first premise establishes a universal statement and the second premise applies that statement to a specific case. Therefore, the conclusion can be logically deduced. \\boxed\{valid\}

Q: If it is raining, then the ground is wet. The ground is wet. Therefore, it must be raining. Is this argument valid or invalid?

A: This argument is invalid because it commits the fallacy of affirming the consequent. Just because the ground is wet does not necessarily mean that it is raining, as there could be other factors that caused the ground to become wet. \\boxed\{invalid\}

Solve the Initial Problem:

Let’s solve the following reasoning problem:

Q: "Is Siri a stepsister of Mary? Is Susan related to Kate? In large families, it is sometimes difficult to keep track of all one’s relatives. The following argument seeks to clarify some such relations: To start with, everyone who is a schoolmate of Mildred is a daughter of Jeanette, too. Now, being a daughter of Jeanette is sufficient for not being a cousin of Cristi. Therefore, no schoolmate of Mildred is a cousin of Cristi." Is the argument, given the explicitly stated premises, deductively valid or invalid?

A: The argument is deductively valid. The premises state that everyone who is a schoolmate of Mildred is a daughter of Jeanette, and being a daughter of Jeanette is sufficient for not being a cousin of Cristi. Therefore, it logically follows that no schoolmate of Mildred is a cousin of Cristi. \\boxed\{valid\}

Below is a baseline output generated by GPT3.5-turbo using 0-shot CoT prompt. This output does not recall any relevant exemplars and adopts an incorrect approach to address the deductive reasoning problem.

The argument is deductively invalid.

To determine the validity of the argument, we need to analyze the logical structure and see if the conclusion necessarily follows from the premises.

Let’s break down the argument:

1. Everyone who is a schoolmate of Mildred is a daughter of Jeanette.

2. Being a daughter of Jeanette is sufficient for not being a cousin of Cristi.

Conclusion: No schoolmate of Mildred is a cousin of Cristi.

The first premise establishes a relationship between being a schoolmate of Mildred and being a daughter of Jeanette. However, it does not provide any information about the relationship between being a schoolmate of Mildred and being a cousin of Cristi.

The second premise establishes a relationship between being a daughter of Jeanette and not being a cousin of Cristi. However, it does not provide any information about the relationship between being a schoolmate of Mildred and being a cousin of Cristi.

Therefore, the conclusion that no schoolmate of Mildred is a cousin of Cristi cannot be logically derived from the given premises. The argument is deductively invalid.

\\boxed\{invalid\}