FunSearch：利用大语言模型在数学科学领域探索新奇发现 [译]

通过搜索编写在计算机代码中的“函数”，FunSearch 利用大语言模型 (LLMs) 首次在数学科学的未解之谜中取得突破

大语言模型作为高效的辅助工具，它们擅长综合不同的概念，并能通过阅读、写作和编程来协助人们解决难题。但它们是否能够揭示全新的知识呢？

尽管大语言模型可能会产生不符合事实的“幻觉”信息，利用它们来做出可以被证实正确的发现确实是一大挑战。但如果我们能够发掘并利用大语言模型中最具创造力的想法呢？

今天，我们在《自然》杂志发表的一篇论文中介绍了 FunSearch，这是一种在数学和计算机科学领域寻找创新解决方案的新方法。FunSearch 结合了一种预先训练好的大语言模型（LLM）和一个自动“评估器”。这个 LLM 的目标是提供以计算机代码形式呈现的创新性解决方案，而评估器则负责防止错误或虚构的想法。通过这两部分的反复迭代，最初的解决方案得以“进化”成全新的知识。系统通过搜索用计算机代码编写的“函数”来进行工作，因此命名为 FunSearch。

这是首次利用大语言模型（LLM）在科学或数学的复杂开放性问题中取得新发现。FunSearch 解决了数学中一个历史悠久的开放性问题——帽子集问题，并提出了新的解决方案。不仅如此，为了证明 FunSearch 的实际应用价值，我们还利用它发现了解决“装箱”问题的更高效算法。这个问题广泛应用于许多领域，例如提高数据中心的效率。

科学进步始终依赖于新知识的共享。FunSearch 作为一种强大的科学工具，其独特之处在于它不仅展示了解决方案本身，还展示了这些解决方案是如何构建出来的。我们希望，FunSearch 能够激发使用它的科学家们进一步的思考，从而推动持续的改进和新发现。

利用语言模型推动创新发现的进化过程

FunSearch 运用大语言模型 (LLM) 驱动的进化方法，专注于培养和发展高评分的创意。这些创意被转化为可自动运行和评估的计算机程序。首先，用户需用代码描述问题，包括一个用于评估程序的流程和一个初始化程序池的初始程序。

FunSearch 是一个循环迭代的过程。在每一轮中，系统会从现有程序池选取若干程序，交由 LLM 加工。LLM 在这些程序的基础上进行创新，生成新程序，并自动对它们进行评估。表现最佳的程序将被重新加入程序池，形成一个自我提升的循环。FunSearch 主要使用谷歌的 PaLM 2，但也兼容其他基于代码的大语言模型。

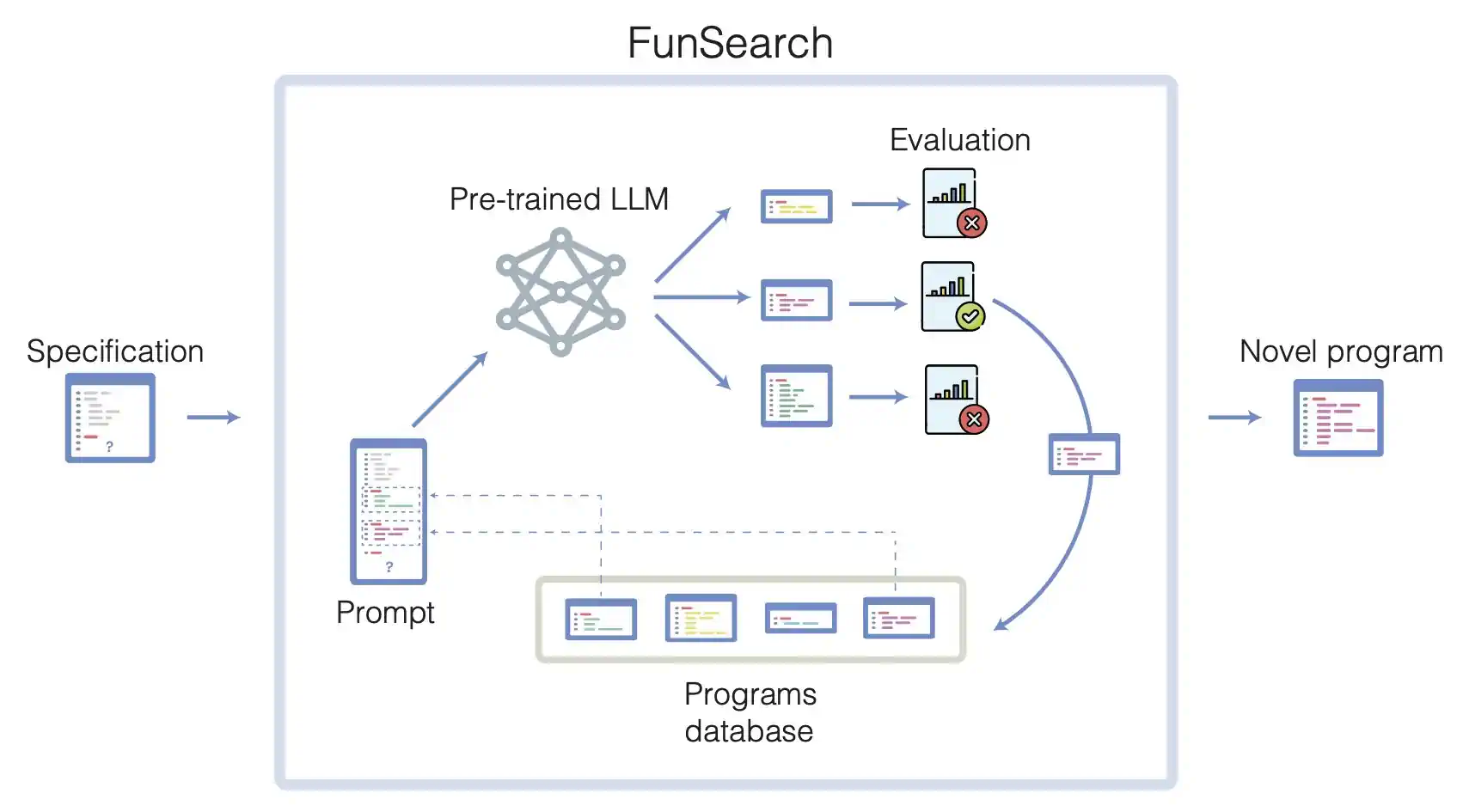
FunSearch 的运作流程。LLM 被展示了迄今为止生成的最佳程序（从程序库中提取），并被要求生成更优秀的程序。LLM 提出的程序会自动执行并进行评估，表现最佳者将被加入数据库，供下一轮循环选择。用户随时可以获取到目前发现的最高分程序。

在不同领域探索新的数学知识和算法是极具挑战性的任务，往往超出当前最先进的 AI 系统所能及。为应对 FunSearch 中的这些难题，我们引入了几个关键组件。我们不是从零开始，而是基于对问题的基本认识启动进化过程，使 FunSearch 能集中精力寻找关键创意，推动新发现。此外，我们的进化流程还特别注重创意的多样性，避免陷入思维僵局。最后，通过并行运行进化过程，我们提高了系统的效率。

数学界的新突破

我们着手解决了一个长期以来让多个数学研究领域的学者们头疼的难题——帽子集问题。这个问题被著名数学家 Terence Tao 形容为他最感兴趣的悬而未决的问题。在这一领域，我们与威斯康星大学麦迪逊分校的数学教授、该问题关键性突破的作者 Jordan Ellenberg 进行了合作。

帽子集问题的核心在于，在一个高维网格中找出最大的点集（即“帽子集”），条件是这些点中任意三个不共线。这个问题之所以关键，是因为它在极端组合学（extremal combinatorics）——一门研究数字、图表或其他对象可能的最大或最小集合规模的学科——中扮演了一个模型角色。采用传统的暴力计算方法来解决这个问题是行不通的，因为所需处理的数据量很快就会超过宇宙中所有原子的总数。

FunSearch 创造了解决方案——以程序的形式出现——在某些情况下找到了迄今为止最大的帽子集。这标志着过去 20 年中帽子集规模的最大增长。更重要的是，FunSearch 在性能上超越了当前最先进的计算求解器，因为这个问题的规模远超它们的处理能力。

这些成果不仅证明了 FunSearch 技术在解决复杂的组合问题方面取得了超越传统成果的进步，在这些领域内构建直觉通常相当困难。我们期待这种方法在解决组合学中类似的理论问题时发挥重要作用，并有望在未来为通信理论等领域带来新的突破。

FunSearch：追求简洁且易于人类理解的程序

在数学领域，新知识的发现本身就具有重大意义。FunSearch 方法在此基础上，相较于传统的计算机搜索技术，提供了更为显著的优势。FunSearch 的独特之处在于，它不仅仅是生成问题的解决方案，更重要的是，它能够生成描述解决方案的得出过程的程序。这种“展示过程”的方法正是科学家们探索新发现或现象时的常用手段，他们会通过解释产生这些发现的过程来进行阐述。

FunSearch 专注于寻找由高度精简程序表示的解决方案，即具有低柯尔莫戈洛夫复杂度的解决方案。这些简短的程序能够描述庞大的对象，使得 FunSearch 能够应对那些在广阔数据海洋中寻找特定目标的难题。此外，这还使得 FunSearch 生成的程序结果更易于研究者理解。Ellenberg 教授这样评价 FunSearch：“它为我们提供了全新的解题策略。FunSearch 所产生的解决方案不仅仅是一些数字的堆砌，它们在概念上更为丰富深邃。研究这些解决方案，我能学到更多东西”。

更进一步，FunSearch 程序的可解释性为研究人员提供了实用的洞见。在使用 FunSearch 的过程中，我们发现了一些高分输出代码中的奇特对称性。这些发现为我们提供了对问题的全新理解，并指导我们改进提给 FunSearch 的问题，从而获得了更优的解决方案。我们认为，这种人机合作的方式将成为解决数学领域众多问题的典范。

FunSearch 所生成的解决方案不仅仅是数字的堆砌，在概念上它们更加丰富。研究它们，我能学到很多东西。

—— JORDAN ELLENBERG，威斯康星大学麦迪逊分校的合作伙伴和数学教授

应对计算领域的硬骨头问题

在理论上成功解决 cap set 问题后，我们转向探索 FunSearch 的灵活性，并将其应用于计算机科学中的实际重大挑战。"bin packing"（箱子打包）问题涉及如何将大小不一的物品尽可能少地装入箱子中。这个问题是许多实际应用的核心，例如集装箱装载和数据中心的计算任务分配，目的是降低成本。

在线的 bin-packing 问题一般依靠基于人类经验的启发式算法来解决。但为每种不同的情况 - 如不同的大小、时间或容量 - 制定一套规则是个挑战。虽然这个问题与 cap set 问题大相径庭，但使用 FunSearch 来处理却相当简单。FunSearch 自动生成了适应特定数据的程序，并且效率超过了传统启发式方法 - 它用更少的箱子装下了同样多的物品。

像在线 bin packing 这样的复杂组合问题也可以通过其他 AI 方法来解决，例如神经网络和强化学习。这些方法同样有效，但可能需要大量资源来部署。相比之下，FunSearch 输出的代码易于检查和部署，这意味着其解决方案可能迅速适用于各种实际工业系统，快速带来好处。

大语言模型驱动下的科学发现及其它领域

FunSearch 显示了，只要妥善处理大语言模型可能出现的幻觉问题，我们就能利用这些模型的能力不仅在数学上取得新的发现，还能为解决重要的现实世界问题提供潜在的有影响力的解决方案。

我们预见，在科学和工业界，许多长期存在的或新出现的问题将通过大语言模型驱动的方法来生成有效和量身定制的算法，这将成为常规做法。

事实上，这仅仅是个开始。随着大语言模型进步的步伐，FunSearch 也将自然提升。我们还将致力于拓展其功能，以应对社会面临的各种紧迫科学和工程挑战。