涌现能力的深刻理解:基础现象、幻觉,或两者皆有? [译]
![涌现能力的深刻理解:基础现象、幻觉,或两者皆有? [译]](https://windowsontheory.files.wordpress.com/2023/12/cartoon_landscape.png?w=656\&h=300\&crop=1)
在语言模型的发展中,我们见证了规模的强大力量。Radford 等人在最初的 GPT 论文 中指出,模型在训练过程的某个时刻突然“习得”了对句子 X 进行情感分析的能力,能预测它更可能是“非常消极”或“非常积极”的后续内容。随着模型的训练,其零样本 (zero-shot) 性能出现了显著的“飞跃”。当然,如 Radford 等人所述,这需要一个“成本高昂的预训练步骤——在 8 个 GPU 上训练 1 个月”。😊

图 1: 图片改编自 OpenAI GPT 博客文章 (2018 年)。
GPT-2 论文 揭示了规模增大的益处。正如论文所述,GPT-2 是对 GPT 的扩展版本,拥有大约十倍的参数和数据量。这种规模的扩大带来了质的飞跃。尤其是不仅提高了“零样本”性能,还能生成较长的连贯文本(见下文)。当然,GPT-3 和 GPT-4 进一步证明了规模的重要性。

图 2: GPT-2 根据 Open-AI 博客文章生成的文本。

图 3: GPT 3.5-turbo-instruct 根据同一文本生成的内容。

图 4: GPT-4 对于撰写同一篇演讲的提示作出的回应。
Wei et al. 的研究表明,随着训练规模的增大,“涌现的能力”是常见现象。这种新能力的特征是:
- 当我们按训练计算量(对数刻度)绘制性能曲线时,最初的阶段性能表现平平,但在某个临界点后,性能会突然大幅提升。
- 我们目前无法预先准确预测这个临界点的出现时间。

图 5: 出自 Ganguli et al 关于“可预测性与意外”研究的图 2。左侧面板基于 GPT-3 论文,中间面板基于 Gopher 论文,右侧面板基于 Nye et al, 21。
“Grokking 文章”(作者:Power et al)也展示了在代数任务的合成环境中,从随机猜测到完美解决问题的显著进步。
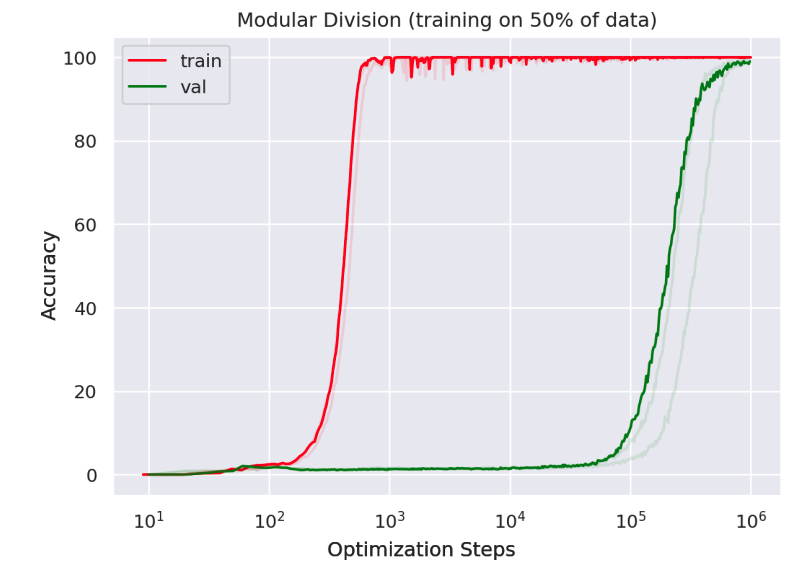
图 6: 一种深度网络在学习模块化除法时,展现了从基本水平到完美准确度的显著提升。更重要的是,这种转变在测试精度上的出现比训练精度要晚得多。详见 Power et al 的图 1。
涌现能力真的是幻觉吗?
近期,Schaffer, Miranda, 和 Koyejo 的一篇论文中提出了这样一个观点:涌现能力可能只是一种错觉。他们指出,如果换一个评估任务表现的标准,我们可能会看到一个平缓且可预期的进步,而不是之前认为的突兀和难以预测的飞跃。
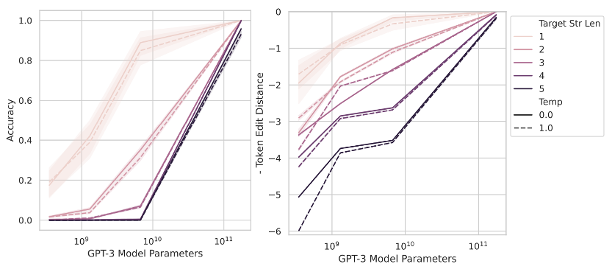
图 7:根据输出长度来衡量两个四位数相加的表现,分别采用(左侧)准确性:完全正确答案的比率,和(右侧)编辑距离:与正确答案的接近程度。右侧图表中的“软”指标展示出了一种比左侧的“硬”指标更为逐步和可预测的进展。摘自 Schaeffer et al, 2023 的图 3。
我们自己的论文(与 Edelman, Goel, Kakade, Malach, 和 Zhang 合作)也展现了类似的现象,即在学习奇偶性任务时也观察到这样的情况。而 Nanda et al 则使用了机械可解释性方法,为“理解”这一概念提出了一个“进程度量”。

图 8: 改编自 Barak et al. 22 的图 3。尽管错误率和损失在图中突然下降,但在学习奇偶性问题时,相关特征权重的变化却更为渐进。
可以通过以下类比来理解这一现象:想象有人正在学习跳过一个一米高的跨栏。
图 9: ChatGPT (DALL-E) 绘制的漫画,展现了一位志在成为跨栏高手的运动员。
当这位梦想成为优秀运动员的人不断训练时,他们的跳跃高度理应不断提高。但如果我们通过他们越过栏杆的可能性来评估他们的进步,就会发现一种“急剧转变”或“新技能突显”的趋势。

图 10: 运动员跳跃的高度随着训练量的增加而逐渐提高,但越过一米高栏杆的概率却会出现明显的跳跃式增长。
在他们引人入胜的论文中,Schaffer、Miranda 和 Koyejo 展示了如何通过改变评估标准,让很多看似突然出现的技能曲线消失不见。那么,这是否意味着所有新技能的显现都只是错觉呢?我认为并非如此。
这是因为,在现实世界中的许多任务,尤其是涉及推理的任务,我们需要同时应对多重挑战。特别是在构建一条连续的“思考链”时,我们必须依次解决一系列问题,一旦其中任何一环出错,都可能导致整个推理偏离正确轨道。Schaffer 等人在论文的第二节中指出,当成功的条件变为多个因素共同满足(即多事件的“并且”关系)时,成功的概率曲线会变得更加陡峭。


图 11: 当单枚硬币出现“正面”的概率增加时,所有 k 枚硬币同时出现“正面”的概率急剧提高。(上图:X 轴代表单枚硬币出现正面的概率,下图:X 轴为单枚硬币概率的对数值,即 (p,1-p) 与 (1,0) 的负交叉熵损失)
在很多实际任务中,我们往往不知道如何把一个复杂的任务拆解成一系列简单、可预测的小部分,特别是在我们还未解决这个任务之前。因此,即便我们能精确地预测一个用 N flops 训练出的模型的损失值,我们也可能无法预测这个模型能解决哪些任务,尤其是那些超出仅需 N/10 flops 的模型所能解决的任务。
