亲手制作 transformer:无需训练! [译]
Theia Vogel
目标读者:对大语言模型(LLM/Large Language Model)有一定了解,对 Transformer 的工作原理感兴趣(但可能对矩阵知识有些生疏)
一直以来,我都希望能更深入地理解 Transformer 和注意力(attention)机制。虽然我阅读了《插图版 Transformer》,但我仍旧对于注意力机制的各个部分如何运作缺乏直观感受。例如 q 和 k 之间的区别,更不用说 v 了!
因此,我决定亲手制作一个 Transformer 来预测一个简单序列(具体来说,是一个类似于 GPT-2 的仅解码器结构的 Transformer)——不是通过训练或使用预先训练的权重,而是通过逐个手动分配权重,仅用了一晚上的时间。结果证明,这个方法有效!现在,我对 Transformer 的理解更加深刻,希望通过这篇文章,你也能有所收获。
我们需要做的基本步骤包括:
- 选择一个适中的任务——既不要太简单,也不要像“编写流畅英文文本”那样复杂,后者至少需要几百万参数。
- 为任务选择合适的模型维度
- 设计位置(
wpe)和 Token(wte)嵌入的权重 - 最具挑战性的部分——设计一个 Transformer 块来执行实际计算!
- 首先,我们需要一个
c_attn层来生成q、k和v矩阵 - 接着,我们需要一个
c_proj层来将这个结果重新投影到嵌入层
- 首先,我们需要一个
- 最后,利用之前的 Token 嵌入权重(
wte)来生成下一个 Token 的概率对数!
矩阵运算简介
我们将会进行大量的矩阵运算,包括标量加法/乘法和矩阵乘法(Python 中的 @ 运算符)。如果你不太熟悉数学或机器学习领域,或者感觉有些生疏,这里有一个简洁的矩阵数学概述供你参考。如果你对此已经有足够的了解,可以跳过这部分。
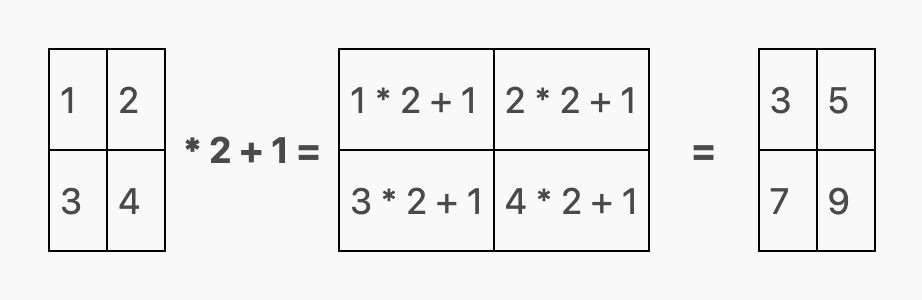
标量加法和乘法指的是将一个数值分别加到或乘以矩阵中的每一个元素上:
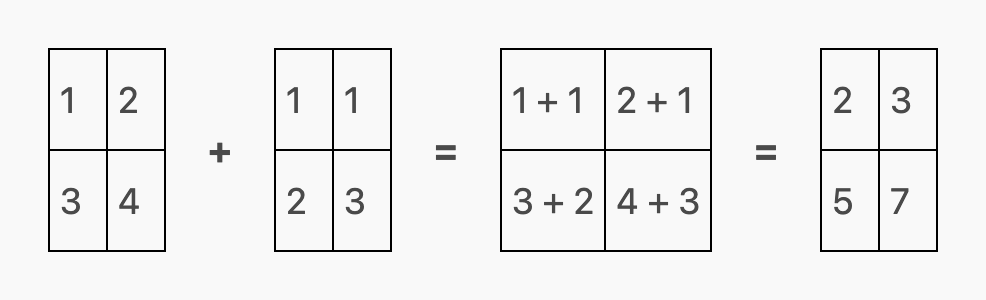
两个矩阵的加法或减法也被定义为每个矩阵中相应元素之间的元素向操作:

在矩阵乘法中,除了标准的 矩阵积 之外,还有一种 元素逐个相乘 的操作方式。通常所说的矩阵乘法指的是矩阵积,这种方式将形状为 A x B 和 B x C 的两个矩阵合并,生成一个 A x C 维度的新矩阵。
比如,一个 2 行 4 列(2 x 4)的矩阵可以与一个 4 行 3 列(4 x 3)的矩阵相乘,因为第一个矩阵的列数(4)与第二个矩阵的行数相同,最终产生一个 2 行 3 列(2 x 3)的矩阵。
实际的计算过程是,对输出矩阵中每个位置对应的行和列进行点积运算,即计算它们的元素对应相乘后的和。
比如,在下面的示例中,我们用红色标记的行和列来计算输出矩阵中的红色单元格,绿色单元格的计算方式相同:
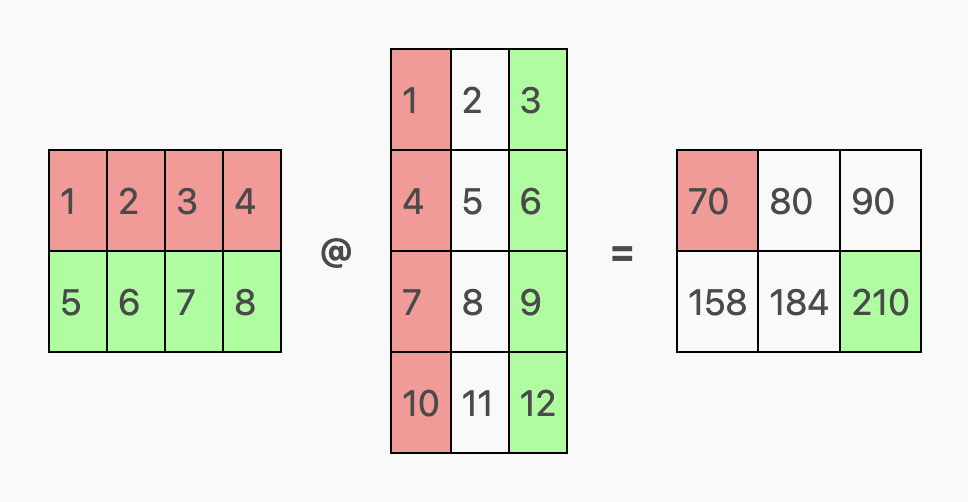
对于输出矩阵中的红色单元格(第 0 行,第 0 列),我们取第一个矩阵的红色行(第 0 行)和第二个矩阵的红色列(第 0 列),计算它们的点积(1*1 + 2*4 + 3*7 + 4*10),结果为 70。
同理,对于输出矩阵中的绿色单元格(第 1 行,第 2 列),我们取第一个矩阵的绿色行(第 1 行)和第二个矩阵的绿色列(第 2 列),计算它们的点积(5*3 + 6*6 + 7*9 + 8*12),结果为 210。
选择任务
最初,我的任务只是预测类似于 "ababababab" 这样的序列。但我很快发现,由于 Transformer (Transformer) 预测的是 向后移动一位 的序列,这个任务过于简单,不需要利用位置嵌入 (position embeddings)。简而言之,算法就是“如果当前是 a,就预测 b;否则预测 a”。
后来,我决定挑战一个更复杂的任务,预测序列 "aabaabaabaab...",即 (aab)* 的重复模式。这个任务要求查询前两个 Token (Token) 来确定输出是 a(如果前两个 Token 是 ab 或 ba)还是 b(如果前两个 Token 是 aa)。
岔路:设计一种标记化方案
考虑到我们只处理两个符号,我采用了一个简单的标记化方案:a 对应 0,b 对应 1:
CHARS = ["a", "b"]def tokenize(s): return [CHARS.index(c) for c in s]def untok(tok): return CHARS[tok]# examples:tokenize("aabaa") # => [0, 0, 1, 0, 0]untok(0) # => "a"untok(1) # => "b"
选择模型
我基于 jaymody 的 picoGPT 实现的 GPT-2 进行了一些简化修改1。这些修改帮助我确定了权重分配的架构。如果你对此还不太明白,不用担心,我们会在后续内容中逐步解释!
# based on https://github.com/jaymody/picoGPT/blob/main/gpt2.py (MIT license)import numpy as npdef softmax(x):exp_x = np.exp(x - np.max(x, axis=-1, keepdims=True))return exp_x / np.sum(exp_x, axis=-1, keepdims=True)# [m, in], [in, out], [out] -> [m, out]def linear(x, w, b):return x @ w + b# [n_q, d_k], [n_k, d_k], [n_k, d_v], [n_q, n_k] -> [n_q, d_v]def attention(q, k, v, mask):return softmax(q @ k.T / np.sqrt(q.shape[-1]) + mask) @ v# [n_seq, n_embd] -> [n_seq, n_embd]def causal_self_attention(x, c_attn, c_proj):# qkv projectionsx = linear(x, **c_attn) # [n_seq, n_embd] -> [n_seq, 3*n_embd]# split into qkvq, k, v = np.split(x, 3, axis=-1) # [n_seq, 3*n_embd] -> 3 of [n_seq, n_embd]# causal mask to hide future inputs from being attended tocausal_mask = (1 - np.tri(x.shape[0], dtype=x.dtype)) * -1e10 # [n_seq, n_seq]# perform causal self attentionx = attention(q, k, v, causal_mask) # [n_seq, n_embd] -> [n_seq, n_embd]# out projectionx = linear(x, **c_proj) # [n_seq, n_embd] @ [n_embd, n_embd] = [n_seq, n_embd]return x# [n_seq, n_embd] -> [n_seq, n_embd]def transformer_block(x, attn):x = x + causal_self_attention(x, **attn)return x# [n_seq] -> [n_seq, n_vocab]def gpt(inputs, wte, wpe, blocks):# token + positional embeddingsx = wte[inputs] + wpe[range(len(inputs))] # [n_seq] -> [n_seq, n_embd]# forward pass through n_layer transformer blocksfor block in blocks:x = transformer_block(x, **block) # [n_seq, n_embd] -> [n_seq, n_embd]# project to vocabreturn x @ wte.T # [n_seq, n_embd] -> [n_seq, n_vocab]
这大致对应于以下的架构图:
确定模型的关键参数
我们需要确定三个主要的模型参数:
- 上下文长度
- 词汇量大小
- 嵌入大小
上下文长度指的是模型一次性处理的最大 Token 数量。理论上,这项任务仅需要考虑前两个 Token——但为了增加难度,我们选择使用 5 个 Token,这样模型还需忽略那些不相关的 Token。
词汇量大小是指模型能识别的不同 Token 的总数。在实际模型中,需要在泛化能力、不同 Token 数量的学习、上下文长度的使用等方面进行权衡。但我们的任务相对简单,因此只需使用两种 Token:a(0)和 b(1)。
嵌入大小是模型学习每个 Token/位置的向量尺寸,也是模型内部使用的尺寸。我随意选择了 8,恰巧这就是所需的大小 :-)
总的来说,
N_CTX = 5N_VOCAB = 2N_EMBED = 8
您提供的内容已完成翻译。如果您有更多翻译需求,欢迎随时提供新的内容。
设计嵌入权重
设计过程首先是将 token id 列表([0, 1, 0, ...])转化为一个 seq_len x embedding_size 的矩阵,这个矩阵融合了每个 token(Token)的位置和类型:
def gpt(inputs, wte, wpe, blocks): # [n_seq] -> [n_seq, n_vocab]# token + positional embeddingsx = wte[inputs] + wpe[range(len(inputs))] # [n_seq] -> [n_seq, n_embd]...
这就意味着我们首先需要设计的是 wte(token 嵌入的权重)和 wpe(位置嵌入的权重2)。我们将采用一种 1-hot 编码方案,即每一类事物在一个独特的位置上有一个 1。
例如,我们将使用前五个嵌入元素来创建位置的 1-hot 编码:位置 0 表示为 [1, 0, 0, 0, 0],位置 1 为 [0, 1, 0, 0, 0],以此类推,直到位置 4 的 [0, 0, 0, 0, 1]。
同理,我们用接下来的两个嵌入元素来创建 token id 的 1-hot 编码:token a 表示为 [1, 0],token b 为 [0, 1]。
MODEL = {"wte": np.array(# one-hot token embeddings[[0, 0, 0, 0, 0, 1, 0, 0], # token `a` (id 0)[0, 0, 0, 0, 0, 0, 1, 0], # token `b` (id 1)]),"wpe": np.array(# one-hot position embeddings[[1, 0, 0, 0, 0, 0, 0, 0], # position 0[0, 1, 0, 0, 0, 0, 0, 0], # position 1[0, 0, 1, 0, 0, 0, 0, 0], # position 2[0, 0, 0, 1, 0, 0, 0, 0], # position 3[0, 0, 0, 0, 1, 0, 0, 0], # position 4]),...: ...,}
如果我们用这种编码方式处理整个序列 "aabaa",我们会得到一个形状为 5 x 8(seq_len x embedding_size)的嵌入矩阵:

这样,我们就得到了模型其余部分将会使用的嵌入矩阵,直到最后阶段它再被映射回词汇空间。值得注意的是,第七个位置留空了——这将在 Transformer 块中作为临时空间使用。接下来讲讲...
设计 Transformer 块
虽然模型代码支持多个 Transformer 块,但我们此处只用一个。每个 Transformer 块包括两个部分:一个注意力机制头部(attention head),和一个线性网络,后者负责将注意力机制处理后的结果矩阵再投影回常规的 seq_len x embedding_size 矩阵。
首先来看看注意力机制头部。
设计注意力头部
注意力头部是 Transformer 块的核心组成部分——这是注意力处理发生的地方。正如那句名言:“注意力就是一切!”
(大多数现代 Transformer 在每个 Transformer 块中都配备了多个并行的头部(即“多头注意力”),这也是“注意力头部”一词的由来。但为了简化,我们这里只用一个头部。在这个上下文中,“注意力头部”等同于注意力层。)
如你所料,注意力头部的关键就是注意力。在我们的案例中,注意力被定义为:
# [n_q, d_k], [n_k, d_k], [n_k, d_v], [n_q, n_k] -> [n_q, d_v]def attention(q, k, v, mask):return softmax(q @ k.T / np.sqrt(q.shape[-1]) + mask) @ v
这其中涉及的参数包括:
q(查询)k(键)v(值)- 还有
mask,这是一个非学习型参数,用来在训练期间防止模型作弊,比如提前看到未来的 Token。这个概念后面会详细解释。
通常我们会通过类比字典查找来解释这些参数:
DICT = { k: v }DICT[q]
...但我发现这种解释并不太易懂。实际上理解注意力是如何工作的,会让这个概念更加清晰——让我们深入探索一下!
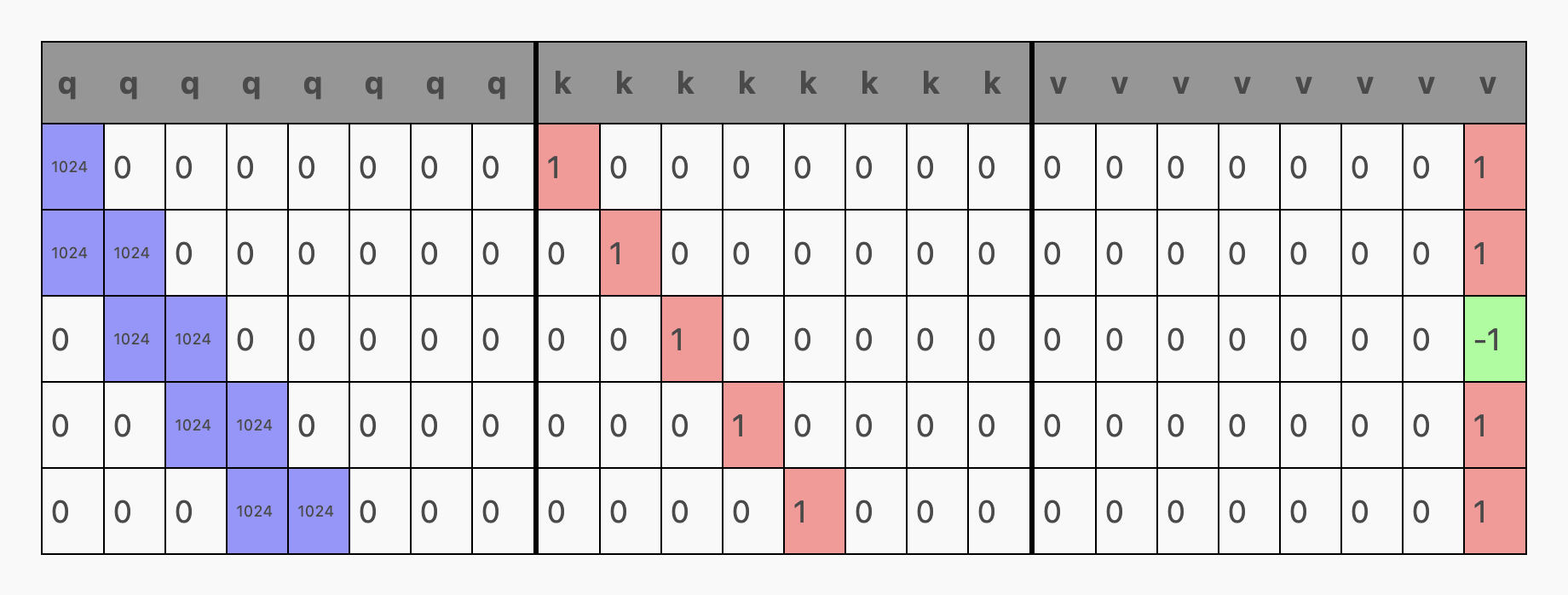
在我们的模型中,注意力的权重是通过 c_attn 来定义的:
Lg = 1024 # LargeMODEL = {...: ...,"blocks": [{"attn": {"c_attn": { # generates qkv matrix"b": np.zeros(N_EMBED * 3),"w": np.array(# this is where the magic happens# fmt: off[[Lg, 0., 0., 0., 0., 0., 0., 0., # q1., 0., 0., 0., 0., 0., 0., 0., # k0., 0., 0., 0., 0., 0., 0., 0.], # v[Lg, Lg, 0., 0., 0., 0., 0., 0., # q0., 1., 0., 0., 0., 0., 0., 0., # k0., 0., 0., 0., 0., 0., 0., 0.], # v[0., Lg, Lg, 0., 0., 0., 0., 0., # q0., 0., 1., 0., 0., 0., 0., 0., # k0., 0., 0., 0., 0., 0., 0., 0.], # v[0., 0., Lg, Lg, 0., 0., 0., 0., # q0., 0., 0., 1., 0., 0., 0., 0., # k0., 0., 0., 0., 0., 0., 0., 0.], # v[0., 0., 0., Lg, Lg, 0., 0., 0., # q0., 0., 0., 0., 1., 0., 0., 0., # k0., 0., 0., 0., 0., 0., 0., 0.], # v[0., 0., 0., 0., 0., 0., 0., 0., # q0., 0., 0., 0., 0., 0., 0., 0., # k0., 0., 0., 0., 0., 0., 0., 1.], # v[0., 0., 0., 0., 0., 0., 0., 0., # q0., 0., 0., 0., 0., 0., 0., 0., # k0., 0., 0., 0., 0., 0., 0., -1], # v[0., 0., 0., 0., 0., 0., 0., 0., # q0., 0., 0., 0., 0., 0., 0., 0., # k0., 0., 0., 0., 0., 0., 0., 0.], # v]# fmt: on),},...: ...,}}]}
虽然看起来有些复杂,但实际上 c_attn 只是一个常规的全连接层,其维度为 embed_size x (embed_size * 3)。当我们将其与之前计算的 seq_len x embed_size 的嵌入矩阵相乘时,就会得到一个 seq_len x (embed_size * 3) 大小的矩阵,我们称之为 qkv 矩阵。这个 qkv 矩阵接着被分割成三个 seq_len x embed_size 大小的矩阵:q、k 和 v。
def causal_self_attention(x, c_attn, c_proj):# qkv projectionsx = linear(x, **c_attn) # [n_seq, n_embd] -> [n_seq, 3*n_embd]# split into qkvq, k, v = np.split(x, 3, axis=-1) # [n_seq, 3*n_embd] -> 3 of [n_seq, n_embd]...
(在上述权重中,我将 c_attn 的权重按不同的行排列,以便展示哪些权重分别生成了 qkv 矩阵中的 q、k、v 部分。)
现在,让我们将之前的嵌入矩阵通过 c_attn 运行一遍,看看会发生什么!如果我们取出嵌入...

...当我们通过 embedding @ c_attn["w"] + c_attn["b"] 处理后,得到一个 5 x 24 (seq_len x (embed_size * 3)) 的 qkv 矩阵。这里的粗线表示我们接下来会用 np.split 来分割这个矩阵:
现在先不考虑 v,我们来关注 q 和 k。
k 的含义比较明确——它仅仅是从综合嵌入矩阵中提取出的独热编码位置嵌入。你可以将其理解为每个 Token 所“代表”的位置信息。
那么 q 是什么呢?如果说 k 是每个 Token 所提供的信息,那么 q 就是每个 Token 所寻求的信息——但这在实际中是如何运作的呢?3 实际上,在注意力机制中,k 被转置并与 q 相乘,在 q @ k.T 的过程中,形成一个 seq_len x seq_len 的矩阵:
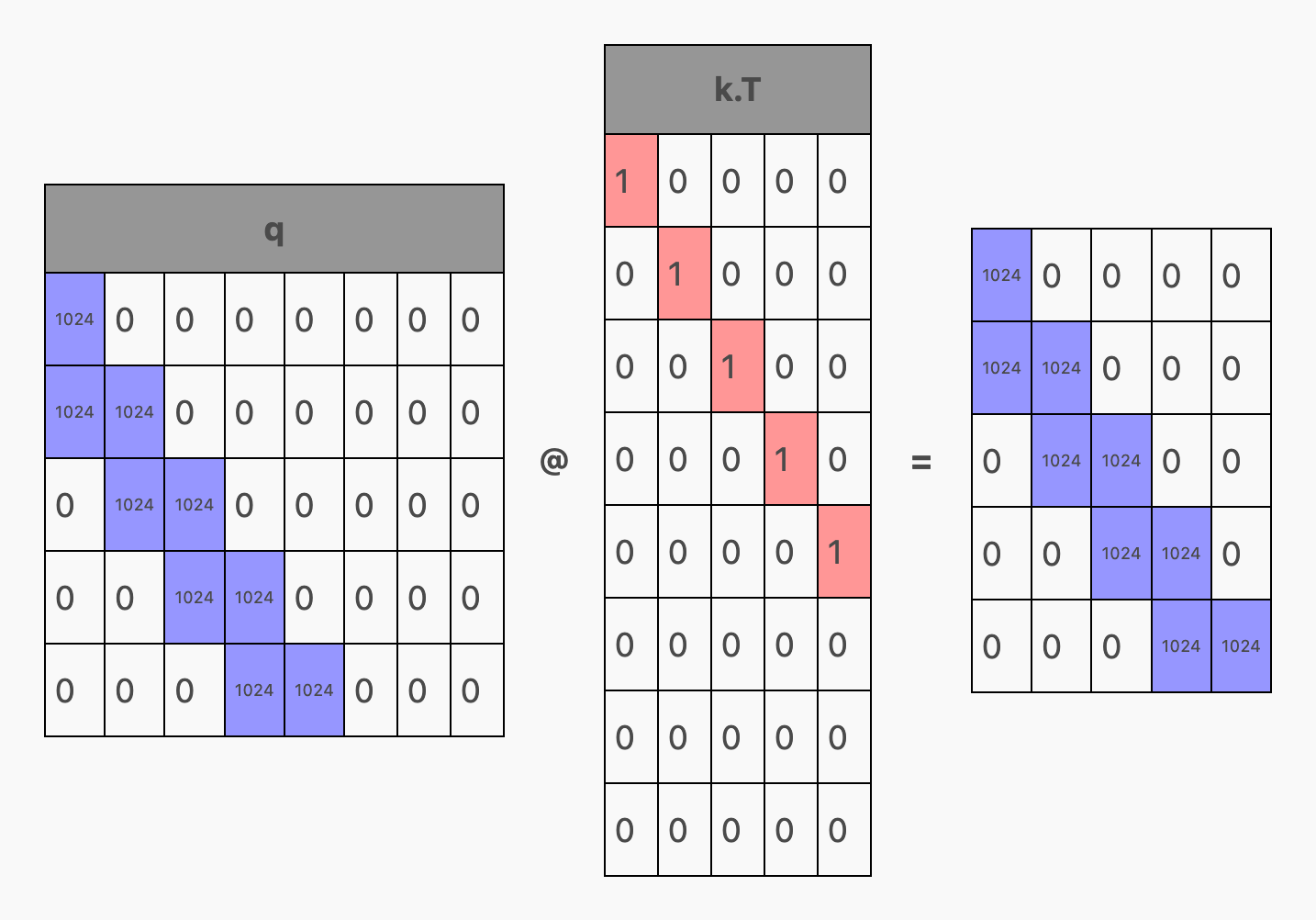
...当我们加入掩码并对整个公式应用 softmax 函数 (softmax(q @ k.T + mask)) 后,这一切突然变得明晰起来!
对 softmax 的简要介绍
Softmax 的定义如下:
def softmax(x):exp_x = np.exp(x - np.max(x, axis=-1, keepdims=True))return exp_x / np.sum(exp_x, axis=-1, keepdims=True)
这个公式看似复杂!但如果你仔细分析,它实际上在执行的是:
- 对于矩阵中的每一行(
axis = -1)... - 从每行的其他元素中减去最大值(这样除了最大值为 0,其他元素都会是负数)
- 为每个元素计算指数值(
matrix[i, j] = e^matrix[i, j])- 这样最大的元素变为 1,因为
e^0 = 1 - 稍小于最大值的数值将接近 1,比如
e^-0.5 ≈ 0.6 - 远小于最大值的数值将接近 0,比如
e^-10 ≈ 0.00004。
- 这样最大的元素变为 1,因为
- 最终,将行中的每个元素除以该行所有元素的总和,以便行的总和为 1(可作为概率分布使用)
我们对每行进行独立处理,因为在模型中,每行代表一个独立的输入 Token 及其对应的预测概率。
下面是 softmax 操作的一个示例:
请注意,在每行中,数值最大的元素总是获得 softmax 结果中最大的比例。但如果这个数值远大于行中的其他数值,它几乎会占据整行的总和。另外,值得注意的是,行中最大值的绝对大小并不重要,重要的是它与其他值的相对大小。这是因为我们在处理的第一步就是减去最大值,所以一行 [10, 0, 0] 最终会变成 [0, -10, -10]。
对 softmax 的一个直观理解是,它类似于一个更加平滑的 argmax 函数:argmax 函数会将最大的元素映射为 1,其余元素映射为 0,而 softmax 则是一个更温和的版本,它会将一部分比重分配给其他位置。

把每行看作是生成该行预测所需的信息(例如,第 0 行包含了看到第一个 Token 后模型进行预测所需的信息),而每列则表示模型应该关注的 Token。此外,重要的是要记住,掩码机制确保了模型不能“预见”未来的信息。(我将在接下来解释这一点。)
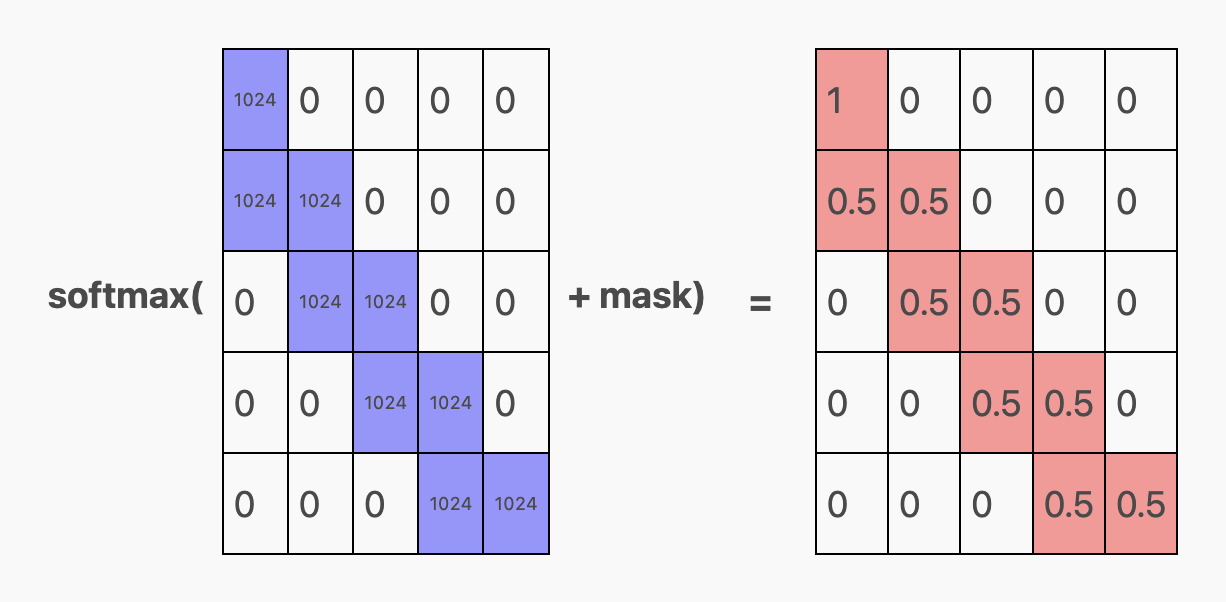
这段内容解释了,对于第一个预测(即第 0 行),模型只能关注第一个 token,因此它把全部注意力集中在这个 token 上。具体来说,就是第一行第一列是 1,其他位置都是零。
而对于其余的预测,模型至少有两个 token 可供关注。在 aabaabaab... 的任务中,最多需要关注两个 token 就够了。因此,模型会把注意力平均分配给最近的两个未被遮蔽的 token。例如,对第二个 token 的预测(第 1 行)同时关注 token 0 和 token 1,对第三个 token 的预测(第 3 行)关注 token 1 和 token 2,以此类推。我们可以看到,每个相关单元格中都有 0.5。
接下来谈谈 mask 这个术语,它被加入到 softmax(q @ k.T + mask) 中。它的作用是什么呢?简单来说,它就是下面这样一个矩阵:

mask 的作用是防止模型在常规梯度下降训练过程中作弊。如果没有 mask,模型可能会根据第二个 token 的值来预测第一个 token,这显然是不合理的。通过添加一个极小的值 -∞4,模型在被遮蔽的(即未来的)token 位置上的注意力会被压制,从而在 softmax 输出的矩阵中这些位置上的值为 0。这迫使模型真正学会如何预测这些位置,而不是通过提前“窥视”来作弊。在我们的例子中,由于这个手工制作的 Transformer 不是为了作弊而设计的,mask 实际上并没有起作用,但它的存在使模型更接近真正的 GPT-2 架构。
最后,关于 mask 和缩放:在实际训练中,通过 np.sqrt(q.shape[-1]) 进行缩放可以产生更好的梯度,但这对我们的手工制作的 Transformer 没有影响。重要的是 softmax(q @ k.T / np.sqrt(q.shape[-1]) + mask) 的计算结果是:

首先简单回顾一下,这里的每一行表示模型在预测某个位置(即预测下一个 Token)时,会关注不同 Token 位置(即列)的程度。例如,为了预测第一个 Token(也就是预测第二个 Token),我们只能关注第一个 Token。而为了预测第二个 Token(预测第三个 Token),我们则需要将注意力分配在第一和第二个 Token 上,以此类推。
但这里的 v 又代表什么呢?注意力机制的最后一步是把前面的矩阵与 v 相乘:softmax(q @ k.T / np.sqrt(q.shape[-1]) + mask) @ v,重点在于 @ v。那么 v 到底是什么?
回想一下之前的嵌入矩阵...
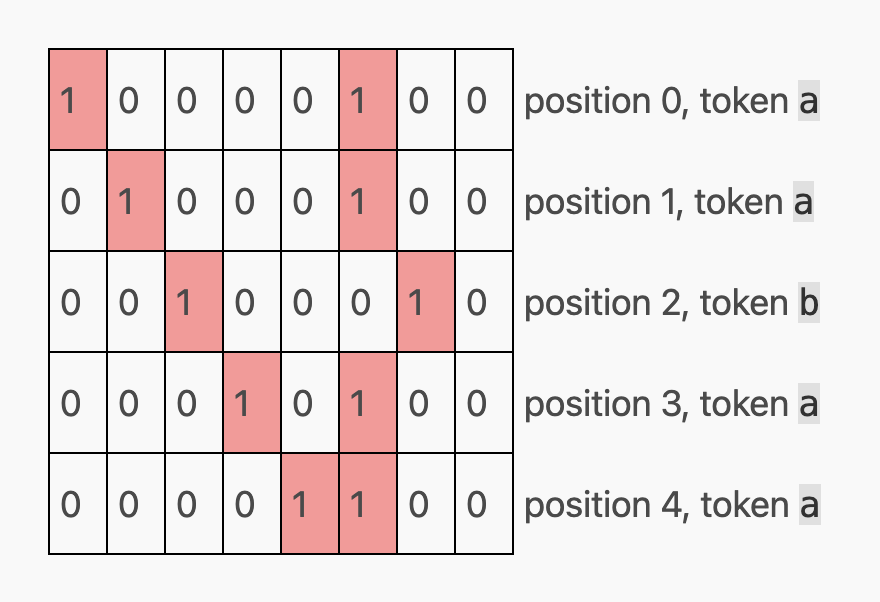
...通过 linear 函数和 c_attn 参数,我们得到了所谓的 qkv 矩阵:
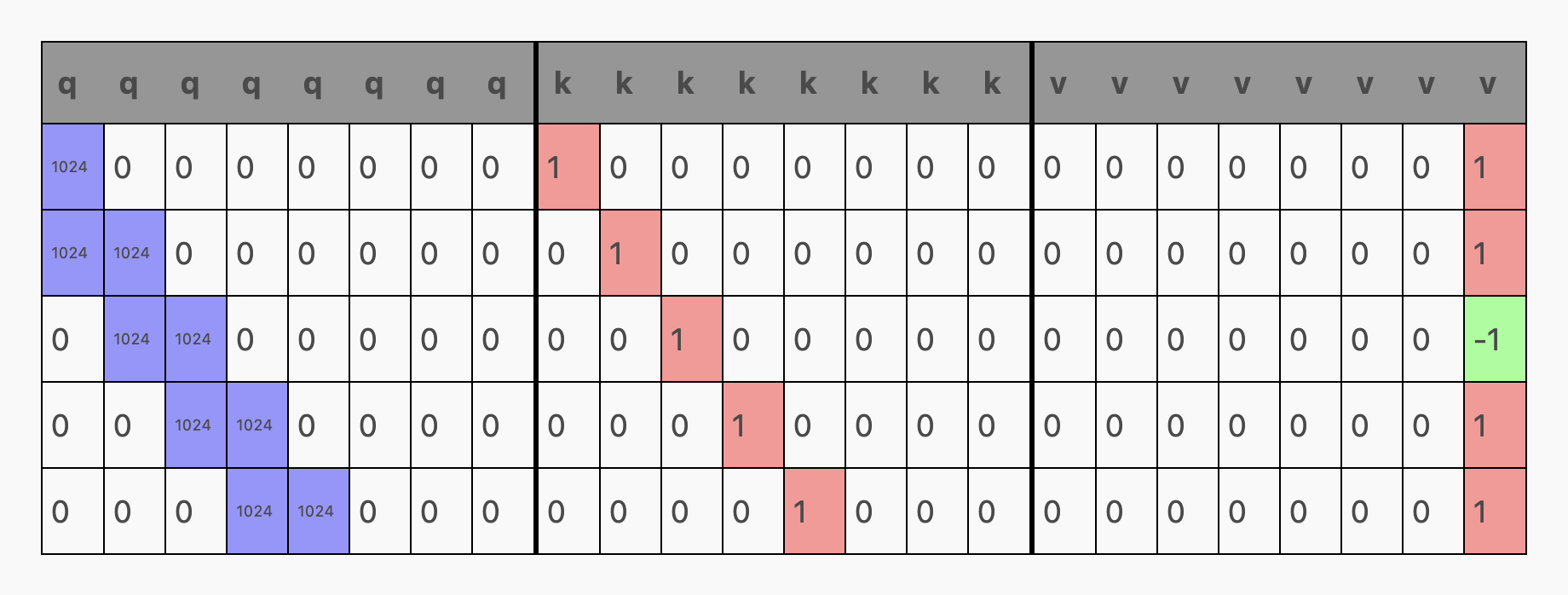
仔细观察 v 的部分,我们发现它只在一个元素(第 7 列)上有设置,这个元素在行代表 a Token 时为 1,而在行代表 b Token 时则为 -1。这意味着 v 的作用只是将单热 Token 编码(a = [1, 0], b = [0, 1])转换成了 1 和 -1 的编码形式!
虽然这听起来似乎没什么大用,但请记住,我们的任务是预测序列 aabaab,也就是说:
- 如果前面的 Token 是(a, a),则预测 b
- 如果前面的 Token 是(a, b),则预测 a
- 如果前面的 Token 是(b, a),则预测 a
- 如果前面的 Token 是(b, b),则预测错误,因为这超出了我们的预测范围。
考虑到我们可以安全地将 (b, b) 情况排除在外,这意味着我们只在关注的 Token 相同时才预测 b Token!因为矩阵乘法涉及加法,我们可以利用加法的消去效应,也就是说:0.5 + 0.5 = 1 和 0.5 + (-0.5) = 0。
通过将 a 编码为 1,b 编码为 -1,这个简单方程恰好满足了我们的需求。当需要预测的 Token 应该是 a 时,这个方程等于 0;而当预测应该是 b 时,方程等于 1:
- a, b → 0.5 * 1 + 0.5 * (-1) = 0
- b, a → 0.5 * (-1) + 0.5 * 1 = 0
- a, a → 0.5 * 1 + 0.5 * 1 = 1
如果我们对之前的 softmax 结果矩阵和之前分出的 v 矩阵进行相乘,对每一行执行这样的计算,我们可以得到输入序列 aabaa 的以下注意力结果:
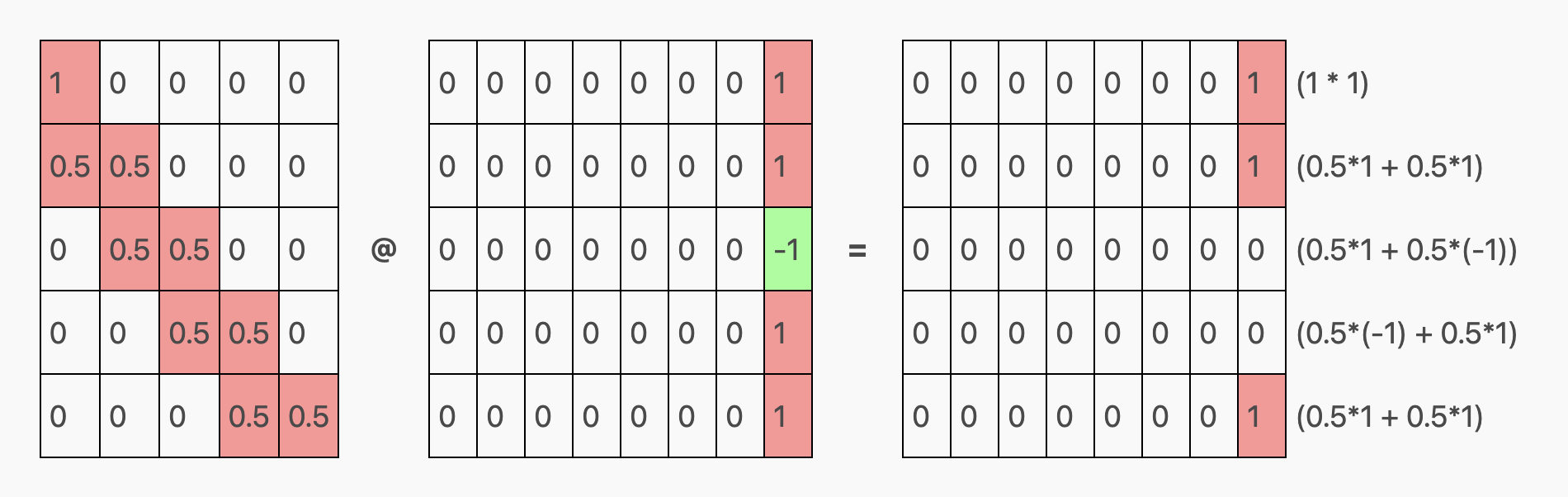
第一行预测出一个不必要的 b,因为它的数据不足(仅依靠一个 a Token,结果可能是 a 或 b)。但其余两个对 b 的预测非常准确:第二行预测下一个 Token 是 b,这是正确的;最后一行预测序列之后的 Token 也是 b,同样正确。
总结来说,c_attn 权重的作用是:
- 将位置嵌入映射到查询向量
q的一个特殊区域,我们称之为“注意力窗口” - 从
k(键向量)中提取位置嵌入 - 把 Token 的嵌入转换成
v(值向量)中的一种特殊编码,即1/-1编码 - 当我们将
q和k在softmax(q @ k.T / ... + mask)公式中结合,就会产生一个seq_len x seq_len的矩阵- 在这个矩阵的第一行,模型仅关注第一个 Token
- 在矩阵的其他行,模型会平等地关注最近的两个 Token
- 最终,通过
softmax(...) @ v的运算,模型利用加法原理来实现预测- 当需要预测
a时,矩阵某行的第 7 个位置会是0 - 当需要预测
b时,该位置会是1
- 当需要预测
(从生物学的角度来看,这个过程可以类比为抑制剂和促进剂的作用:在关注的 Token 中,a 的出现促进了第 7 位置的活跃,而 b 的出现则抑制了它。)
经过这些步骤,我们的注意力机制头部就构建完成了!
投射回嵌入空间的处理
我们接下来要完成的是 Transformer 块的最后一步:将注意力机制的输出结果转换回标准的嵌入形式。在我们的模型中,注意力头会把预测结果放在 embedding[row, 7] 位置(对 b 为 1,对 a 为 0)。然而,我们通常使用一种称为独热编码的方法,这种方法中,embedding[row, 5] 的正值代表 a,embedding[row, 6] 的正值代表 b。
由于一些马上会明了的原因,我们不想这一层仅产生普通的独热编码(比如 [..., 1, 0, ...] 或 [..., 0, 1, ...] 这样的形式)。相反,我们希望得到一种 缩放 过的独热编码,例如 [..., 1024, 0, ...] 或 [..., 0, 1024, ...]。
为了实现这一点,我们只需调整 c_proj 层的偏置(bias),使得 embedding[row, 5](代表 Token a 的位置)默认为 1024。然后,我们将注意力机制的结果 embedding[row, 7] 适当缩放并引入:
Lg = 1024 # LargeMODEL = {"wte": ...,"wpe": ...,"blocks": [{"attn": {"c_attn": ...,"c_proj": { # weights to project attn result back to embedding space"b": [0, 0, 0, 0, 0, Lg, 0, 0],"w": np.array([[0, 0, 0, 0, 0, 0, 0, 0],[0, 0, 0, 0, 0, 0, 0, 0],[0, 0, 0, 0, 0, 0, 0, 0],[0, 0, 0, 0, 0, 0, 0, 0],[0, 0, 0, 0, 0, 0, 0, 0],[0, 0, 0, 0, 0, 0, 0, 0],[0, 0, 0, 0, 0, 0, 0, 0],[0, 0, 0, 0, 0, -Lg, Lg, 0],]),},},},],}
简而言之,经过 c_proj 层处理后,
embedding[row, 5](对应于a)的值为Lg + (-Lg) * predictionembedding[row, 6](对应于b)的值为0 + Lg * prediction
当我们将之前的注意力结果通过 c_proj 层处理后,就会得到一个矩阵,这个矩阵正是我们所需要的 —— 经过 1024 缩放的一热预测结果!

完成 c_proj 层的处理后,我们就可以将 Transformer 块的输出结果投射回词汇空间,进行下一步的预测工作!
如何将结果反映回词汇空间并抽取概率
我们的起点是 Transformer 块运行的结果:

这里展示的是将原始嵌入向量与前面提到的 c_prog 的结果相加。原始嵌入被加入的原因是所谓的残差连接:在 transformer_block 中,我们采用 x = x + causal_self_attention(x, ...) 的形式(注意这里有 x +),而不是直接使用 x = causal_self_attention(x, ...)。
残差连接有助于深度网络在多层中保持信息流动。然而,在我们的例子中,它反而造成了干扰。这就是 c_proj 输出被放大 1024 倍的原因:目的是为了压制不必要的残差信号。
接下来,我们将上述矩阵与最初定义的 Token 嵌入权重的转置 (wte) 相乘,以获得最终的 logits:
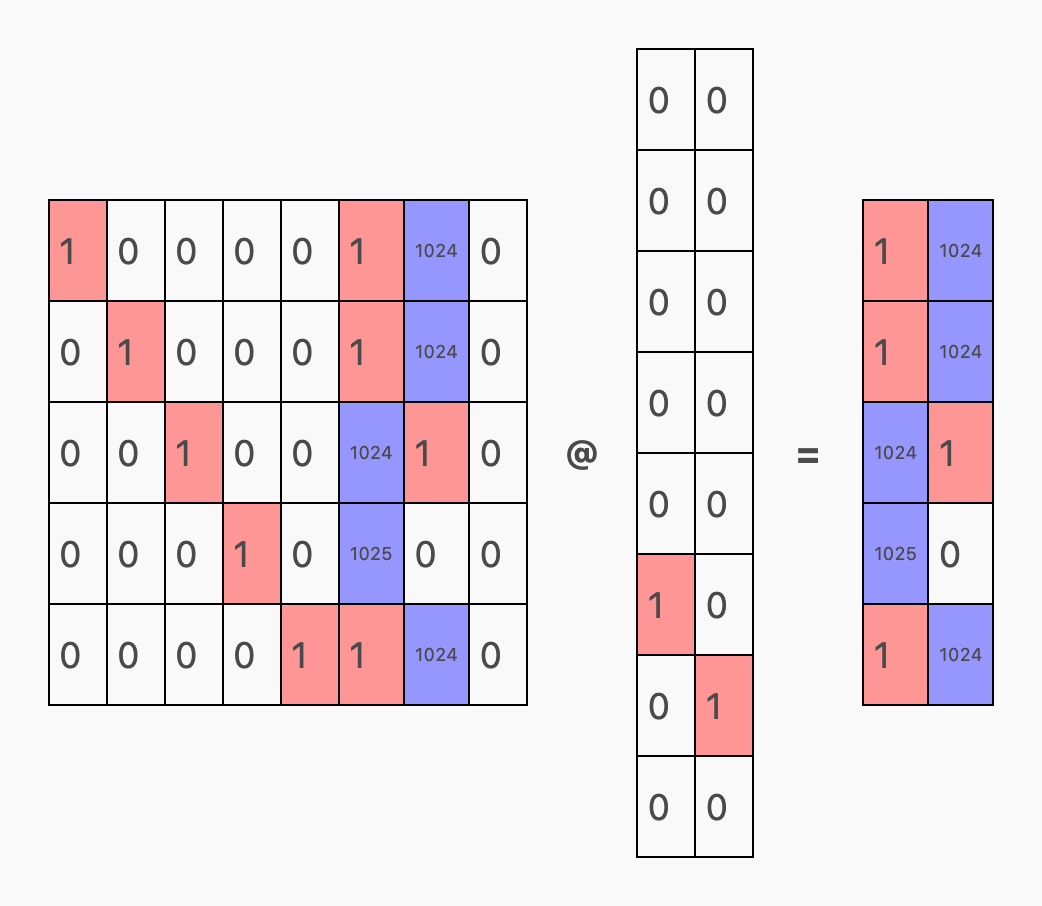
logits 中的红色区域表明,由于残差连接,模型略微倾向于重复某个 Token。但相反的 1024 倍放大作用抑制了这种倾向,因此在经过 softmax 处理后,最终的预测结果完全倾向于单一方向:
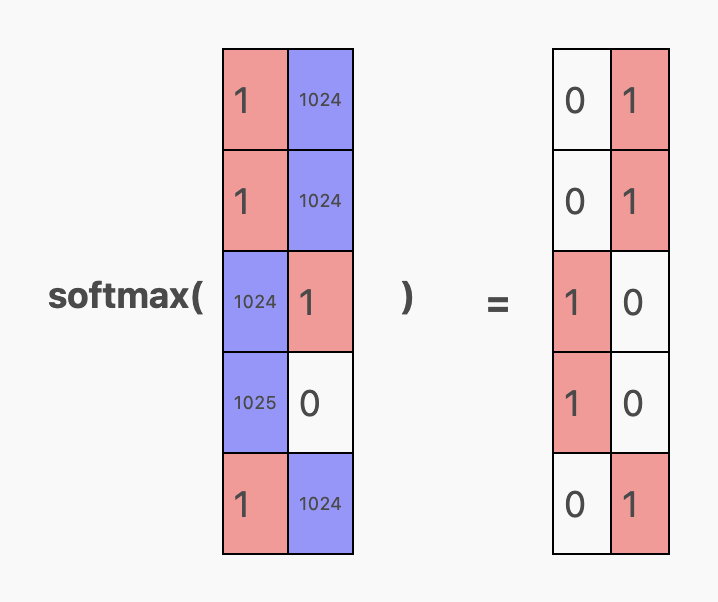
换句话说,当输入上下文序列 aabaa 时,模型的预测如下:
- 在
a之后的 Token 是b(这是可以接受的,因为可能是任意一个) - 在
aa之后的 Token 是b(正确!) - 在
aab之后的 Token 是a(正确!) - 在
aaba之后的 Token 是a(正确!) - 在
aabaa之后的 Token 是b(正确!)
当然,对于推理过程,我们主要关注的是最后一行的预测:b 跟在 aabaa 后面。其他的预测主要用于模型训练。
借助已完成的模型权重(如下),我们可以编写一个简洁的 complete 函数,并证明我们手动构建的模型能够始终生成合理的补全:
def complete(s, max_new_tokens=10):tokens = tokenize(s)while len(tokens) < len(s) + max_new_tokens:logits = gpt(np.array(tokens[-5:]), **MODEL)probs = softmax(logits)pred = np.argmax(probs[-1]) # greedy sample, but temperature sampling would give the same results in our casetokens.append(pred)return s + " :: " + "".join(untok(t) for t in tokens[len(s):])print(complete("a")) # a :: baabaabaabprint(complete("ba")) # ba :: abaabaabaaprint(complete("abaab")) # abaab :: aabaabaaba
它甚至能够从非典型输入中恢复正常!
print(complete("ababa")) # ababa :: abaabaabaaprint(complete("bbbbb")) # bbbbb :: aabaabaaba
如果我们编写一个简单的准确度测试环节,只要提供一个清晰的上下文环境,这个亲手打造的模型可以达到 100% 的准确率:
test = "aab" * 10total, correct = 0, 0for i in range(2, len(test) - 1):ctx = test[:i]expected = test[i]total += 1if untok(predict(ctx)) == expected:correct += 1print(f"ACCURACY: {correct / total * 100}% ({correct} / {total})")# ACCURACY: 100.0% (27 / 27)
结论
感谢您的阅读!希望本文能让您对 Transformer 和注意力机制有了更加直观的理解,也许还会激发您动手尝试制作自己的模型!
如果您对本文感兴趣,可能也会喜欢以下内容:
- 我写的其他博客文章,比如 当 GPT-3 持不同意见时,会忽视工具, 在 Javascript 中,GPT-4 是否能思考得更深入? 以及 我对对抗性训练数据的担忧
- 我的其他项目
- 我的 Twitter,在那里我会分享新的博文、一些关于 AI 的小想法(如 1, 2)和其他动态。
如果您对这篇文章有所感触,请随时与我联系!我非常欢迎和珍视读者的反馈。
致谢
感谢以下朋友审阅了本文的草稿:
完整代码
# Model ops from https://github.com/jaymody/picoGPT/blob/main/gpt2.py (MIT license)import numpy as npdef softmax(x):exp_x = np.exp(x - np.max(x, axis=-1, keepdims=True))return exp_x / np.sum(exp_x, axis=-1, keepdims=True)# [m, in], [in, out], [out] -> [m, out]def linear(x, w, b):return x @ w + b# [n_q, d_k], [n_k, d_k], [n_k, d_v], [n_q, n_k] -> [n_q, d_v]def attention(q, k, v, mask):return softmax(q @ k.T / np.sqrt(q.shape[-1]) + mask) @ v# [n_seq, n_embd] -> [n_seq, n_embd]def causal_self_attention(x, c_attn, c_proj):# qkv projectionsx = linear(x, **c_attn) # [n_seq, n_embd] -> [n_seq, 3*n_embd]# split into qkvq, k, v = np.split(x, 3, axis=-1) # [n_seq, 3*n_embd] -> 3 of [n_seq, n_embd]# causal mask to hide future inputs from being attended tocausal_mask = (1 - np.tri(x.shape[0], dtype=x.dtype)) * -1e10 # [n_seq, n_seq]# perform causal self attentionx = attention(q, k, v, causal_mask) # [n_seq, n_embd] -> [n_seq, n_embd]# out projectionx = linear(x, **c_proj) # [n_seq, n_embd] @ [n_embd, n_embd] = [n_seq, n_embd]return x# [n_seq, n_embd] -> [n_seq, n_embd]def transformer_block(x, attn):x = x + causal_self_attention(x, **attn)# NOTE: removed ffnreturn x# [n_seq] -> [n_seq, n_vocab]def gpt(inputs, wte, wpe, blocks):# token + positional embeddingsx = wte[inputs] + wpe[range(len(inputs))] # [n_seq] -> [n_seq, n_embd]# forward pass through n_layer transformer blocksfor block in blocks:x = transformer_block(x, **block) # [n_seq, n_embd] -> [n_seq, n_embd]# projection to vocabreturn x @ wte.T # [n_seq, n_embd] -> [n_seq, n_vocab]N_CTX = 5N_VOCAB = 2N_EMBED = 8Lg = 1024 # LargeMODEL = {# EMBEDDING USAGE# P = Position embeddings (one-hot)# T = Token embeddings (one-hot, first is `a`, second is `b`)# V = Prediction scratch space## [P, P, P, P, P, T, T, V]"wte": np.array(# one-hot token embeddings[[0, 0, 0, 0, 0, 1, 0, 0], # token `a` (id 0)[0, 0, 0, 0, 0, 0, 1, 0], # token `b` (id 1)]),"wpe": np.array(# one-hot position embeddings[[1, 0, 0, 0, 0, 0, 0, 0], # position 0[0, 1, 0, 0, 0, 0, 0, 0], # position 1[0, 0, 1, 0, 0, 0, 0, 0], # position 2[0, 0, 0, 1, 0, 0, 0, 0], # position 3[0, 0, 0, 0, 1, 0, 0, 0], # position 4]),"blocks": [{"attn": {"c_attn": { # generates qkv matrix"b": np.zeros(N_EMBED * 3),"w": np.array(# this is where the magic happens# fmt: off[[Lg, 0., 0., 0., 0., 0., 0., 0., # q1., 0., 0., 0., 0., 0., 0., 0., # k0., 0., 0., 0., 0., 0., 0., 0.], # v[Lg, Lg, 0., 0., 0., 0., 0., 0., # q0., 1., 0., 0., 0., 0., 0., 0., # k0., 0., 0., 0., 0., 0., 0., 0.], # v[0., Lg, Lg, 0., 0., 0., 0., 0., # q0., 0., 1., 0., 0., 0., 0., 0., # k0., 0., 0., 0., 0., 0., 0., 0.], # v[0., 0., Lg, Lg, 0., 0., 0., 0., # q0., 0., 0., 1., 0., 0., 0., 0., # k0., 0., 0., 0., 0., 0., 0., 0.], # v[0., 0., 0., Lg, Lg, 0., 0., 0., # q0., 0., 0., 0., 1., 0., 0., 0., # k0., 0., 0., 0., 0., 0., 0., 0.], # v[0., 0., 0., 0., 0., 0., 0., 0., # q0., 0., 0., 0., 0., 0., 0., 0., # k0., 0., 0., 0., 0., 0., 0., 1.], # v[0., 0., 0., 0., 0., 0., 0., 0., # q0., 0., 0., 0., 0., 0., 0., 0., # k0., 0., 0., 0., 0., 0., 0., -1], # v[0., 0., 0., 0., 0., 0., 0., 0., # q0., 0., 0., 0., 0., 0., 0., 0., # k0., 0., 0., 0., 0., 0., 0., 0.], # v]# fmt: on),},"c_proj": { # weights to project attn result back to embedding space"b": [0, 0, 0, 0, 0, Lg, 0, 0],"w": np.array([[0, 0, 0, 0, 0, 0, 0, 0],[0, 0, 0, 0, 0, 0, 0, 0],[0, 0, 0, 0, 0, 0, 0, 0],[0, 0, 0, 0, 0, 0, 0, 0],[0, 0, 0, 0, 0, 0, 0, 0],[0, 0, 0, 0, 0, 0, 0, 0],[0, 0, 0, 0, 0, 0, 0, 0],[0, 0, 0, 0, 0, -Lg, Lg, 0],]),},},}],}CHARS = ["a", "b"]def tokenize(s): return [CHARS.index(c) for c in s]def untok(tok): return CHARS[tok]def predict(s):tokens = tokenize(s)[-5:]logits = gpt(np.array(tokens), **MODEL)probs = softmax(logits)for i, tok in enumerate(tokens):pred = np.argmax(probs[i])print(f"{untok(tok)} ({tok}): next={untok(pred)} ({pred}) probs={probs[i]} logits={logits[i]}")return np.argmax(probs[-1])def complete(s, max_new_tokens=10):tokens = tokenize(s)while len(tokens) < len(s) + max_new_tokens:logits = gpt(np.array(tokens[-5:]), **MODEL)probs = softmax(logits)pred = np.argmax(probs[-1])tokens.append(pred)return s + " :: " + "".join(untok(t) for t in tokens[len(s):])test = "aab" * 10total, correct = 0, 0for i in range(2, len(test) - 1):ctx = test[:i]expected = test[i]total += 1if untok(predict(ctx)) == expected:correct += 1print(f"ACCURACY: {correct / total * 100}% ({correct} / {total})")
奖励:效率
对于完整的 5-token 上下文,我们的模型需要大约 4000 次浮点运算来预测一个 token,其中大部分运算用于注意力计算。通过减小上下文窗口、使用融合乘加运算、键值 (kv) 缓存等技术可以减少这一数字,但预测一个 token 仍需数百条机器指令。
相比之下,手写的 (x64) 汇编语言只需八条指令:
; dl: next token; rax: context addr; rcx: context len.next_tokenmov dl, 'a'cmp byte ptr [rax + rcx - 1], 'a'jne .donecmp rcx, 1je .return_bcmp byte ptr [rax + rcx - 2], 'a'jne .done.return_b:mov dl, 'b'.done:
我们能否开发出效率提升 1000 倍的语言模型,即在生成自然语言方面与当前模型相比,就像这段汇编在生成 (aab)* 时那样高效?如果你有解决方案,请给我发邮件。第一个提出方案的人将获得 10 美元的奖励 ;-)
1
如果你对我所做的具体更改感兴趣,它们包括:
- 我去掉了层规范化,因为它们在处理时太麻烦了。我希望能传递一些易于理解的、充满 0 和 1 的矩阵,而层规范化却会把我的
1和0变成1.73200462和-0.57733487:
def layer_norm(x, g, b, eps: float = 1e-5):mean = np.mean(x, axis=-1, keepdims=True)variance = np.var(x, axis=-1, keepdims=True)# normalize x to have mean=0 and var=1 over last axisx = (x - mean) / np.sqrt(variance + eps)return g * x + b # scale and offset with gamma/beta params
(我原本可以通过设置 gamma 来抵消 np.sqrt(...) 的缩放效果,通过设置 beta 来抵消 (x - mean) 的偏移——但我选择了彻底去掉层规范化,而不是每次进行无关更改时都去调整它们。)
- 我使用了单头注意力而不是多头注意力,因为我不需要多个注意力头部。
- 我移除了 Transformer 块中的
mlp前馈层,因为我觉得不需要。(尽管我本可以直接将其设为恒等矩阵。)
2
不同于某些其他的 Transformer 架构,GPT-2 完全使用了通过学习得到的位置嵌入,因此这里没有使用到正弦波或 RoPE。
3
其实,q 和 k 并不一定要分别扮演这些特定的角色。在这篇文章最初的版本里,我把它们的功能对调了:q 被用作位置嵌入(position embeddings)的提取,而 k 则用于查询(query)。不过,按照目前文章中的描述,这种方式更加普遍,而且更符合矩阵的通常命名方式。当然了,GPT-2 对这些名称是闻所未闻的 ;-)
4
实际上,为了避免 NaN 的问题,代码中通常不会直接使用 -∞,而是用 -1e10 这样的数值来代替。不过,这两种做法在实际效果上是一样的。