makeMoE：从零开始打造一个稀疏混合专家语言模型 [译]

概要：本文将带您一步步实现一个稀疏混合专家语言模型。这个项目受到了 Andrej Karpathy 的 'makemore' 项目的启发，并在很大程度上基于它，借鉴了许多可重用的组件。与 'makemore' 类似，'makeMoE' 也是一种自回归的字符级语言模型，但它采用了所谓的稀疏混合专家架构。文章的后续部分将详细介绍这种架构的关键要素及其实现方式。我希望您通过阅读本文并实践代码，能对整个系统的工作原理有一个直观的了解。

您可以在这个 Github 仓库中找到完整的端到端实现：https://github.com/AviSoori1x/makeMoE/tree/main

随着 Mixtral 的发布和关于 Llama 3 可能成为一个混合专家型大语言模型的讨论，这种架构的模型引起了广泛关注。在稀疏混合专家语言模型中，许多组件与传统的 Transformer 模型共享。尽管看似简单，但实证研究表明，这些模型的训练稳定性是主要挑战之一。这样的小规模、可自行调整的实现，有助于快速试验新方法。

在此实现中，我对 'makemore' 的架构做了几项重要更改：

采用稀疏混合专家而非单一前馈神经网络。
引入了 Top-k 门控和带噪声的 Top-k 门控机制。
初始化方面，虽然这里使用了 Kaiming He 初始化，但本项目的目的是便于调整，您可以尝试使用 Xavier/Glorot 初始化等其他方法。

与 'makemore' 相同的部分包括：

数据集、预处理（例如标记化）及 Andrej 最初选择的任务：生成类似莎士比亚风格的文本。
因果自注意力（Casusal self attention）的实现。
训练循环。
推理逻辑。

让我们开始！

稀疏混合专家语言模型，正如预期那样，依靠自注意力机制来理解上下文。接下来，我们将深入探讨专家混合模块的细节。但在此之前，让我们先回顾一下自注意力机制，以加深我们对它的理解。

深入了解因果缩放点积自注意力的直观原理

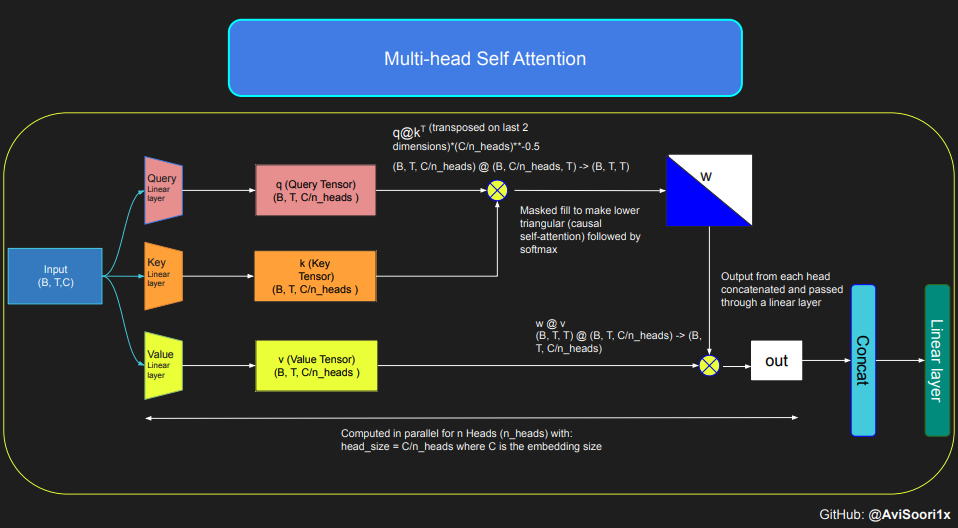
本代码示范了自注意力机制的核心原理，尤其集中于探讨了经典的缩放点积自注意力模型。在这个模型中，查询 (query)、键 (key) 和值 (value) 矩阵均来自同一输入序列。为保证自回归语言生成流程的严谨性，尤其在只有解码器的模型中，本代码使用了特殊的遮盖技术。这一技术极其关键，因为它能够隐藏当前词元位置之后的信息，从而使模型的关注点仅限于序列之前的部分。这种机制被称为因果自注意力。需要指出的是，稀疏专家混合模型并不仅限于仅有解码器的 Transformer 架构。实际上，包括 Shazeer 等人的研究在内，该领域许多重要的工作都集中在 T5 架构上，这种架构涵盖了 Transformer 模型中的编码器和解码器两个部分。

#This code is borrowed from Andrej Karpathy's makemore repository linked in the repo.
The self attention layers in Sparse mixture of experts models are the same as
in regular transformer models

torch.manual_seed(1337)
B,T,C = 4,8,32 # batch, time, channels
x = torch.randn(B,T,C)

# let's see a single Head perform self-attention
head_size = 16
key = nn.Linear(C, head_size, bias=False)
query = nn.Linear(C, head_size, bias=False)
value = nn.Linear(C, head_size, bias=False)
k = key(x)   # (B, T, 16)
q = query(x) # (B, T, 16)
wei =  q @ k.transpose(-2, -1) # (B, T, 16) @ (B, 16, T) ---> (B, T, T)

tril = torch.tril(torch.ones(T, T))
#wei = torch.zeros((T,T))
wei = wei.masked_fill(tril == 0, float('-inf'))
wei = F.softmax(wei, dim=-1) #B,T,T

v = value(x) #B,T,H
out = wei @ v # (B,T,T) @ (B,T,H) -> (B,T,H)
out.shape

torch.Size([4, 8, 16])

关于因果自注意力及其多头版本的代码组织如下所示。多头自注意力通过并行运用多个关注头实现，每个关注头专注于信道的不同部分（即嵌入维度）。通过这种方式，多头自注意力不仅提升了学习效率，也因为其并行性质，大大提高了模型训练的效率。值得一提的是，在这个实现中，我全程使用了 dropout 技术来正则化模型，以避免过拟合问题。

#Causal scaled dot product self-Attention Head
n_embd = 64
n_head = 4
n_layer = 4
head_size = 16
dropout = 0.1

class Head(nn.Module):
    """ one head of self-attention """

    def __init__(self, head_size):
        super().__init__()
        self.key = nn.Linear(n_embd, head_size, bias=False)
        self.query = nn.Linear(n_embd, head_size, bias=False)
        self.value = nn.Linear(n_embd, head_size, bias=False)
        self.register_buffer('tril', torch.tril(torch.ones(block_size, block_size)))

        self.dropout = nn.Dropout(dropout)

    def forward(self, x):
        B,T,C = x.shape
        k = self.key(x)   # (B,T,C)
        q = self.query(x) # (B,T,C)
        # compute attention scores ("affinities")
        wei = q @ k.transpose(-2,-1) * C**-0.5 # (B, T, C) @ (B, C, T) -> (B, T, T)
        wei = wei.masked_fill(self.tril[:T, :T] == 0, float('-inf')) # (B, T, T)
        wei = F.softmax(wei, dim=-1) # (B, T, T)
        wei = self.dropout(wei)
        # perform the weighted aggregation of the values
        v = self.value(x) # (B,T,C)
        out = wei @ v # (B, T, T) @ (B, T, C) -> (B, T, C)
        return out

多头自注意力的具体实现如下：

#Multi-Headed Self Attention
class MultiHeadAttention(nn.Module):
    """ multiple heads of self-attention in parallel """

    def __init__(self, num_heads, head_size):
        super().__init__()
        self.heads = nn.ModuleList([Head(head_size) for _ in range(num_heads)])
        self.proj = nn.Linear(n_embd, n_embd)
        self.dropout = nn.Dropout(dropout)

    def forward(self, x):
        out = torch.cat([h(x) for h in self.heads], dim=-1)
        out = self.dropout(self.proj(out))
        return out

创建简单的多层感知器专家模块

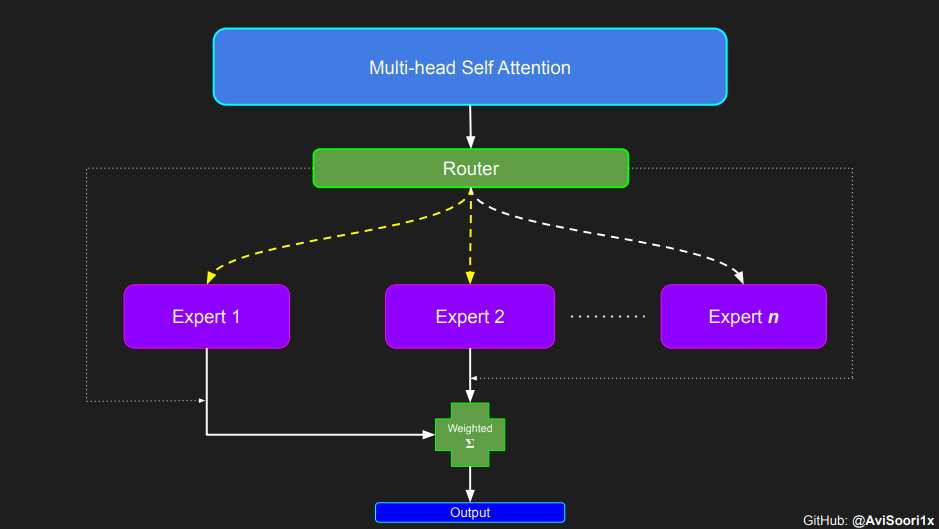
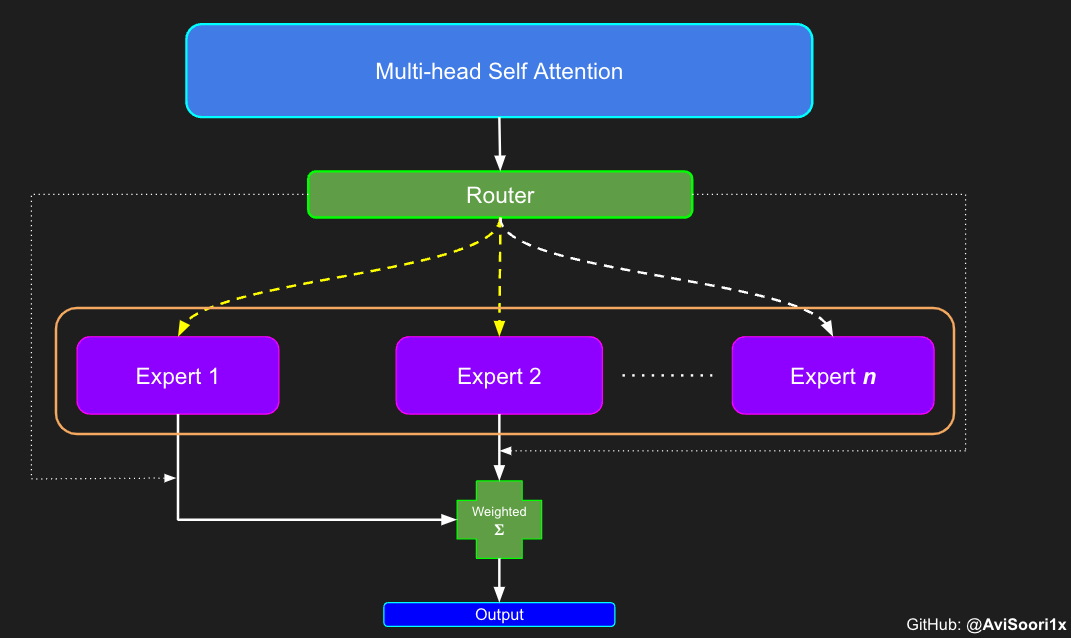
在所谓的稀疏混合专家系统中，每个 Transformer 块中的关注机制并没有改变。但是，每个块的结构发生了一些重要的变化：原本的标准前馈神经网络被一些仅部分激活的前馈网络所取代，这些被称作“专家”。所谓“稀疏激活”是指，序列中的每个 Token 只会被发送给极少数的专家——通常是一个或两个——而不是所有的专家。这种做法有利于提高训练和计算速度，因为在每次处理中只有少数专家被用到。不过，所有的专家模型都需要放在 GPU 内存中，因此，当模型参数的总数达到数千亿甚至数万亿时，就会带来一些独特的部署挑战。

#Expert module
class Expert(nn.Module):
    """ An MLP is a simple linear layer followed by a non-linearity i.e. each Expert """

    def __init__(self, n_embd):
        super().__init__()
        self.net = nn.Sequential(
            nn.Linear(n_embd, 4 * n_embd),
            nn.ReLU(),
            nn.Linear(4 * n_embd, n_embd),
            nn.Dropout(dropout),
        )

    def forward(self, x):
        return self.net(x)

通过一个实例来理解 Top-k 门控机制

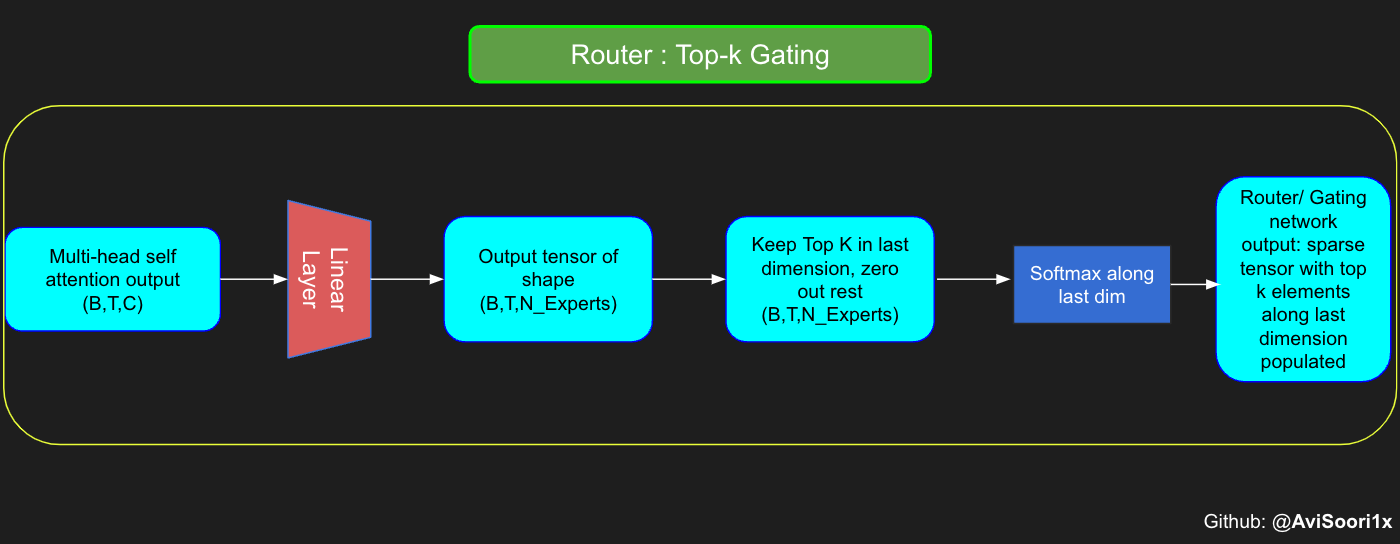
门控网络，也就是我们常说的路由器，它的作用是决定多头注意力机制产生的每个 Token 应该由哪个专家网络处理。让我们通过一个简单的例子来理解这个过程：假设有四个专家网络，我们需要将一个 Token 路由给排名前两位的专家。最开始，我们通过一个线性层将 Token 输入到门控网络。这个层会把输入的张量从一个形状为 (2, 4, 32) — 其中 (2, 4, 32) 代表着 (批大小，Token, n_embed)，n_embed 是输入的通道维度 — 转换成一个新的形状 (2, 4, 4)，即 (批大小，Token, num_experts)，这里的 num_experts 表示专家网络的数量。然后，我们找出最后一个维度上的前 k=2 个最高值及其索引。

#Understanding how gating works
num_experts = 4
top_k=2
n_embed=32


#Example multi-head attention output for a simple illustrative example, consider n_embed=32, context_length=4 and batch_size=2
mh_output = torch.randn(2, 4, n_embed)

topkgate_linear = nn.Linear(n_embed, num_experts) # nn.Linear(32, 4)

logits = topkgate_linear(mh_output)
top_k_logits, top_k_indices = logits.topk(top_k, dim=-1)  # Get top-k experts
top_k_logits, top_k_indices

#output:
(tensor([[[ 0.0246, -0.0190],
          [ 0.1991,  0.1513],
          [ 0.9749,  0.7185],
          [ 0.4406, -0.8357]],

         [[ 0.6206, -0.0503],
          [ 0.8635,  0.3784],
          [ 0.6828,  0.5972],
          [ 0.4743,  0.3420]]], grad_fn=<TopkBackward0>),
 tensor([[[2, 3],
          [2, 1],
          [3, 1],
          [2, 1]],

         [[0, 2],
          [0, 3],
          [3, 2],
          [3, 0]]]))

为了得到稀疏门控输出，我们只保留最后一个维度上的前 k 个值，把其余位置填充为 '-inf'，然后通过 softmax 激活函数处理。这样，'-inf' 的值就会变成零，同时让前两个值变得更加显著，并且它们的和为 1。这样的处理方式有助于对专家网络输出的权重进行合理分配。

zeros = torch.full_like(logits, float('-inf')) #full_like clones a tensor and fills it with a specified value (like infinity) for masking or calculations.
sparse_logits = zeros.scatter(-1, top_k_indices, top_k_logits)
sparse_logits

#output
tensor([[[   -inf,    -inf,  0.0246, -0.0190],
         [   -inf,  0.1513,  0.1991,    -inf],
         [   -inf,  0.7185,    -inf,  0.9749],
         [   -inf, -0.8357,  0.4406,    -inf]],

        [[ 0.6206,    -inf, -0.0503,    -inf],
         [ 0.8635,    -inf,    -inf,  0.3784],
         [   -inf,    -inf,  0.5972,  0.6828],
         [ 0.3420,    -inf,    -inf,  0.4743]]], grad_fn=<ScatterBackward0>)

gating_output= F.softmax(sparse_logits, dim=-1)
gating_output

#ouput
tensor([[[0.0000, 0.0000, 0.5109, 0.4891],
         [0.0000, 0.4881, 0.5119, 0.0000],
         [0.0000, 0.4362, 0.0000, 0.5638],
         [0.0000, 0.2182, 0.7818, 0.0000]],

        [[0.6617, 0.0000, 0.3383, 0.0000],
         [0.6190, 0.0000, 0.0000, 0.3810],
         [0.0000, 0.0000, 0.4786, 0.5214],
         [0.4670, 0.0000, 0.0000, 0.5330]]], grad_fn=<SoftmaxBackward0>)

对上述代码进行泛化和模块化处理，并引入噪声顶尖-k 门控技术以实现有效的负载均衡

# First define the top k router module
class TopkRouter(nn.Module):
    def __init__(self, n_embed, num_experts, top_k):
        super(TopkRouter, self).__init__()
        self.top_k = top_k
        self.linear =nn.Linear(n_embed, num_experts)

    def forward(self, mh_ouput):
        # mh_ouput is the output tensor from multihead self attention block
        logits = self.linear(mh_output)
        top_k_logits, indices = logits.topk(self.top_k, dim=-1)
        zeros = torch.full_like(logits, float('-inf'))
        sparse_logits = zeros.scatter(-1, indices, top_k_logits)
        router_output = F.softmax(sparse_logits, dim=-1)
        return router_output, indices

我们可以通过一些样本输入来测试这一功能：

#Testing this out:
num_experts = 4
top_k = 2
n_embd = 32

mh_output = torch.randn(2, 4, n_embd)  # Example input
top_k_gate = TopkRouter(n_embd, num_experts, top_k)
gating_output, indices = top_k_gate(mh_output)
gating_output.shape, gating_output, indices
#And it works!!

#output
(torch.Size([2, 4, 4]),
 tensor([[[0.5284, 0.0000, 0.4716, 0.0000],
          [0.0000, 0.4592, 0.0000, 0.5408],
          [0.0000, 0.3529, 0.0000, 0.6471],
          [0.3948, 0.0000, 0.0000, 0.6052]],

         [[0.0000, 0.5950, 0.4050, 0.0000],
          [0.4456, 0.0000, 0.5544, 0.0000],
          [0.7208, 0.0000, 0.0000, 0.2792],
          [0.0000, 0.0000, 0.5659, 0.4341]]], grad_fn=<SoftmaxBackward0>),
 tensor([[[0, 2],
          [3, 1],
          [3, 1],
          [3, 0]],

         [[1, 2],
          [2, 0],
          [0, 3],
          [2, 3]]]))

虽然最近发布的 "mixtral" 论文没有提及，但我相信，在训练混合专家模型 (MoE) 的过程中，噪声顶尖-k 门控技术扮演着关键角色。重点在于，我们不希望所有的 token 都集中于同一批受偏爱的专家。我们需要在开发利用和新领域探索之间保持平衡。为了达到负载均衡，向门控线性层输出的 logits 添加标准正态分布噪声是个有效的策略，这有助于提升训练的效率。

]

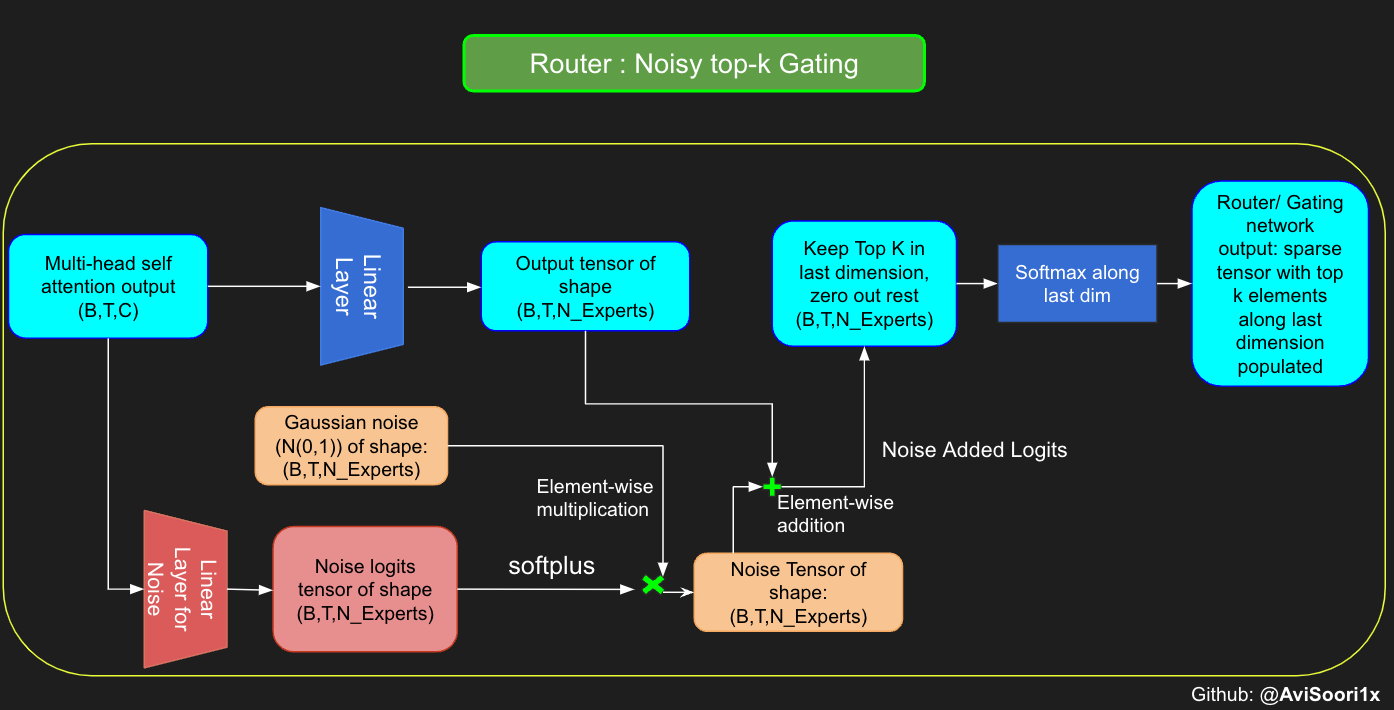
#Changing the above to accomodate noisy top-k gating
class NoisyTopkRouter(nn.Module):
    def __init__(self, n_embed, num_experts, top_k):
        super(NoisyTopkRouter, self).__init__()
        self.top_k = top_k
        #layer for router logits
        self.topkroute_linear = nn.Linear(n_embed, num_experts)
        self.noise_linear =nn.Linear(n_embed, num_experts)


    def forward(self, mh_output):
        # mh_ouput is the output tensor from multihead self attention block
        logits = self.topkroute_linear(mh_output)

        #Noise logits
        noise_logits = self.noise_linear(mh_output)

        #Adding scaled unit gaussian noise to the logits
        noise = torch.randn_like(logits)*F.softplus(noise_logits)
        noisy_logits = logits + noise

        top_k_logits, indices = noisy_logits.topk(self.top_k, dim=-1)
        zeros = torch.full_like(noisy_logits, float('-inf'))
        sparse_logits = zeros.scatter(-1, indices, top_k_logits)
        router_output = F.softmax(sparse_logits, dim=-1)
        return router_output, indices

现在，让我们再次对这个实现进行测试

#Testing this out, again:
num_experts = 8
top_k = 2
n_embd = 16

mh_output = torch.randn(2, 4, n_embd)  # Example input
noisy_top_k_gate = NoisyTopkRouter(n_embd, num_experts, top_k)
gating_output, indices = noisy_top_k_gate(mh_output)
gating_output.shape, gating_output, indices
#It works!!

#output
(torch.Size([2, 4, 8]),
 tensor([[[0.4181, 0.0000, 0.5819, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000],
          [0.4693, 0.5307, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000],
          [0.0000, 0.4985, 0.5015, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000],
          [0.0000, 0.0000, 0.0000, 0.2641, 0.0000, 0.7359, 0.0000, 0.0000]],

         [[0.0000, 0.0000, 0.0000, 0.6301, 0.0000, 0.3699, 0.0000, 0.0000],
          [0.0000, 0.0000, 0.0000, 0.4766, 0.0000, 0.0000, 0.0000, 0.5234],
          [0.0000, 0.0000, 0.0000, 0.6815, 0.0000, 0.0000, 0.3185, 0.0000],
          [0.4482, 0.5518, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000]]],
        grad_fn=<SoftmaxBackward0>),
 tensor([[[2, 0],
          [1, 0],
          [2, 1],
          [5, 3]],

         [[3, 5],
          [7, 3],
          [3, 6],
          [1, 0]]]))

创建稀疏专家混合模块

这一过程的核心在于门控网络的输出。在得到这些结果后，我们会精选出前 k 个值，然后将它们与对应前 k 个专家的输出进行结合。这种精心挑选和结合的过程形成了一个加权总和，这就是稀疏 MoE 模块的输出所在。这个过程最关键也最具挑战性的部分是避免进行无谓的计算。关键是只对最重要的前 k 个专家进行计算，然后基于这些计算得出加权总和。如果对每个专家都进行计算，那么使用稀疏 MoE 的初衷——即实现高效的计算——就无法实现。

class SparseMoE(nn.Module):
    def __init__(self, n_embed, num_experts, top_k):
        super(SparseMoE, self).__init__()
        self.router = NoisyTopkRouter(n_embed, num_experts, top_k)
        self.experts = nn.ModuleList([Expert(n_embed) for _ in range(num_experts)])
        self.top_k = top_k

    def forward(self, x):
        gating_output, indices = self.router(x)
        final_output = torch.zeros_like(x)

        # Reshape inputs for batch processing
        flat_x = x.view(-1, x.size(-1))
        flat_gating_output = gating_output.view(-1, gating_output.size(-1))

        # Process each expert in parallel
        for i, expert in enumerate(self.experts):
            # Create a mask for the inputs where the current expert is in top-k
            expert_mask = (indices == i).any(dim=-1)
            flat_mask = expert_mask.view(-1)

            if flat_mask.any():
                expert_input = flat_x[flat_mask]
                expert_output = expert(expert_input)

                # Extract and apply gating scores
                gating_scores = flat_gating_output[flat_mask, i].unsqueeze(1)
                weighted_output = expert_output * gating_scores

                # Update final output
                # We need to scatter_add the weighted outputs to their original positions in the batch
                final_output.masked_scatter_(expert_mask.unsqueeze(-1), weighted_output)

        return final_output.view_as(x)

实际上运行一下代码来检验这一实现是否有效是个不错的方法。通过以下代码，我们可以看到它的确有效！

import torch
import torch.nn as nn

#Let's test this out
num_experts = 8
top_k = 2
n_embd = 16
dropout=0.1

mh_output = torch.randn(4, 8, n_embd)  # Example multi-head attention output
sparse_moe = SparseMoE(n_embd, num_experts, top_k)
final_output = sparse_moe(mh_output)
print("Shape of the final output:", final_output.shape)

Shape of the final output: torch.Size([4, 8, 16])

特别需要强调的是，理解路由器/门控网络输出中前 k 个专家的重要性是非常关键的，正如上面代码中所展示的。这些前 k 个位置标识了被激活的专家，而在这些前 k 个维度中的值的大小决定了它们的权重比例。这种加权求和的思想在下面的图表中得到了更加明确的阐释。

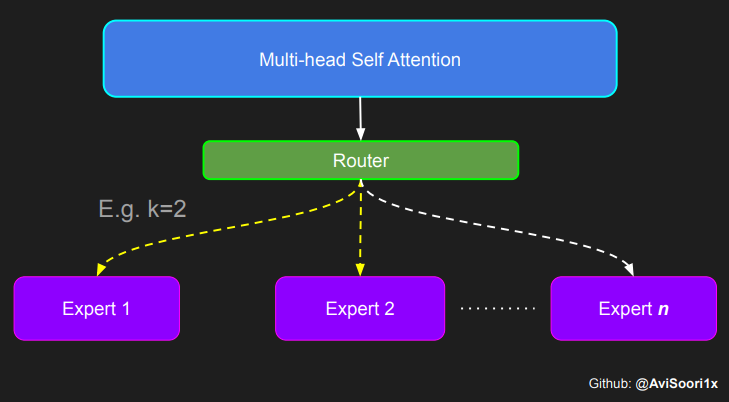
整体构建过程

我们将多头自注意力机制与稀疏混合专家技术相结合，创造了一种新型的 Transformer 架构。这种架构中，我们加入了跳过连接（类似于一种“快捷方式”），以保持训练的稳定性，并避免诸如梯度消失这样的技术难题。此外，我们还使用了层标准化技术来进一步确保学习过程的稳定。

#Create a self attention + mixture of experts block, that may be repeated several number of times
class Block(nn.Module):
    """ Mixture of Experts Transformer block: communication followed by computation (multi-head self attention + SparseMoE) """

    def __init__(self, n_embed, n_head, num_experts, top_k):
        # n_embed: embedding dimension, n_head: the number of heads we'd like
        super().__init__()
        head_size = n_embed // n_head
        self.sa = MultiHeadAttention(n_head, head_size)
        self.smoe = SparseMoE(n_embed, num_experts, top_k)
        self.ln1 = nn.LayerNorm(n_embed)
        self.ln2 = nn.LayerNorm(n_embed)

    def forward(self, x):
        x = x + self.sa(self.ln1(x))
        x = x + self.smoe(self.ln2(x))
        return x

最终，我们成功整合了这些技术，打造出了一款稀疏混合专家语言模型。

class SparseMoELanguageModel(nn.Module):

    def __init__(self):
        super().__init__()
        # each token directly reads off the logits for the next token from a lookup table
        self.token_embedding_table = nn.Embedding(vocab_size, n_embed)
        self.position_embedding_table = nn.Embedding(block_size, n_embed)
        self.blocks = nn.Sequential(*[Block(n_embed, n_head=n_head, num_experts=num_experts,top_k=top_k) for _ in range(n_layer)])
        self.ln_f = nn.LayerNorm(n_embed) # final layer norm
        self.lm_head = nn.Linear(n_embed, vocab_size)

    def forward(self, idx, targets=None):
        B, T = idx.shape

        # idx and targets are both (B,T) tensor of integers
        tok_emb = self.token_embedding_table(idx) # (B,T,C)
        pos_emb = self.position_embedding_table(torch.arange(T, device=device)) # (T,C)
        x = tok_emb + pos_emb # (B,T,C)
        x = self.blocks(x) # (B,T,C)
        x = self.ln_f(x) # (B,T,C)
        logits = self.lm_head(x) # (B,T,vocab_size)

        if targets is None:
            loss = None
        else:
            B, T, C = logits.shape
            logits = logits.view(B*T, C)
            targets = targets.view(B*T)
            loss = F.cross_entropy(logits, targets)

        return logits, loss

    def generate(self, idx, max_new_tokens):
        # idx is (B, T) array of indices in the current context
        for _ in range(max_new_tokens):
            # crop idx to the last block_size tokens
            idx_cond = idx[:, -block_size:]
            # get the predictions
            logits, loss = self(idx_cond)
            # focus only on the last time step
            logits = logits[:, -1, :] # becomes (B, C)
            # apply softmax to get probabilities
            probs = F.softmax(logits, dim=-1) # (B, C)
            # sample from the distribution
            idx_next = torch.multinomial(probs, num_samples=1) # (B, 1)
            # append sampled index to the running sequence
            idx = torch.cat((idx, idx_next), dim=1) # (B, T+1)
        return idx

在深度神经网络的训练过程中，正确的初始化方式至关重要。由于我们的模型中使用了 ReLU 激活函数，因此我们选择了 Kaiming He 初始化方法。同时，你也可以尝试使用在 Transformer 模型中更常见的 Glorot 初始化方法。Jeremy Howard 在 Fastai 的第二部分课程中详细讲解了这些初始化方法的实现：https://course.fast.ai/Lessons/lesson17.html。根据文献，使用 Glorot 初始化可能会进一步提升模型的性能。

def kaiming_init_weights(m):
    if isinstance (m, (nn.Linear)):
        init.kaiming_normal_(m.weight)

model = SparseMoELanguageModel()
model.apply(kaiming_init_weights)

在训练过程中，我利用了 mlflow 这一工具来跟踪和记录重要的训练指标和超参数。我在这里展示的训练循环就包括了这一部分。如果你只想进行简单的训练，不使用 mlflow，可以在 makeMoE 的 GitHub 仓库中找到相应的代码。对于实验和参数追踪，我发现 mlflow 非常实用。

#Using MLFlow
m = model.to(device)
# print the number of parameters in the model
print(sum(p.numel() for p in m.parameters())/1e6, 'M parameters')

# create a PyTorch optimizer
optimizer = torch.optim.AdamW(model.parameters(), lr=learning_rate)
#mlflow.set_experiment("makeMoE")
with mlflow.start_run():
    #If you use mlflow.autolog() this will be automatically logged. I chose to explicitly log here for completeness
    params = {"batch_size": batch_size , "block_size" : block_size, "max_iters": max_iters, "eval_interval": eval_interval,
              "learning_rate": learning_rate, "device": device, "eval_iters": eval_iters, "dropout" : dropout, "num_experts": num_experts, "top_k": top_k }
    mlflow.log_params(params)
    for iter in range(max_iters):

        # every once in a while evaluate the loss on train and val sets
        if iter % eval_interval == 0 or iter == max_iters - 1:
            losses = estimate_loss()
            print(f"step {iter}: train loss {losses['train']:.4f}, val loss {losses['val']:.4f}")
            metrics = {"train_loss": losses['train'], "val_loss": losses['val']}
            mlflow.log_metrics(metrics, step=iter)


        # sample a batch of data
        xb, yb = get_batch('train')

        # evaluate the loss
        logits, loss = model(xb, yb)
        optimizer.zero_grad(set_to_none=True)
        loss.backward()
        optimizer.step()

8.996545 M parameters
step 0: train loss 5.3223, val loss 5.3166
step 100: train loss 2.7351, val loss 2.7429
step 200: train loss 2.5125, val loss 2.5233
.
.
.

step 4999: train loss 1.5712, val loss 1.7508

记录训练和验证过程中的损失值可以帮助我们更好地理解训练进展。从图表中，我们可以看出，在大约 4500 步时停止训练是个不错的选择（因为那时验证损失略有上升）。

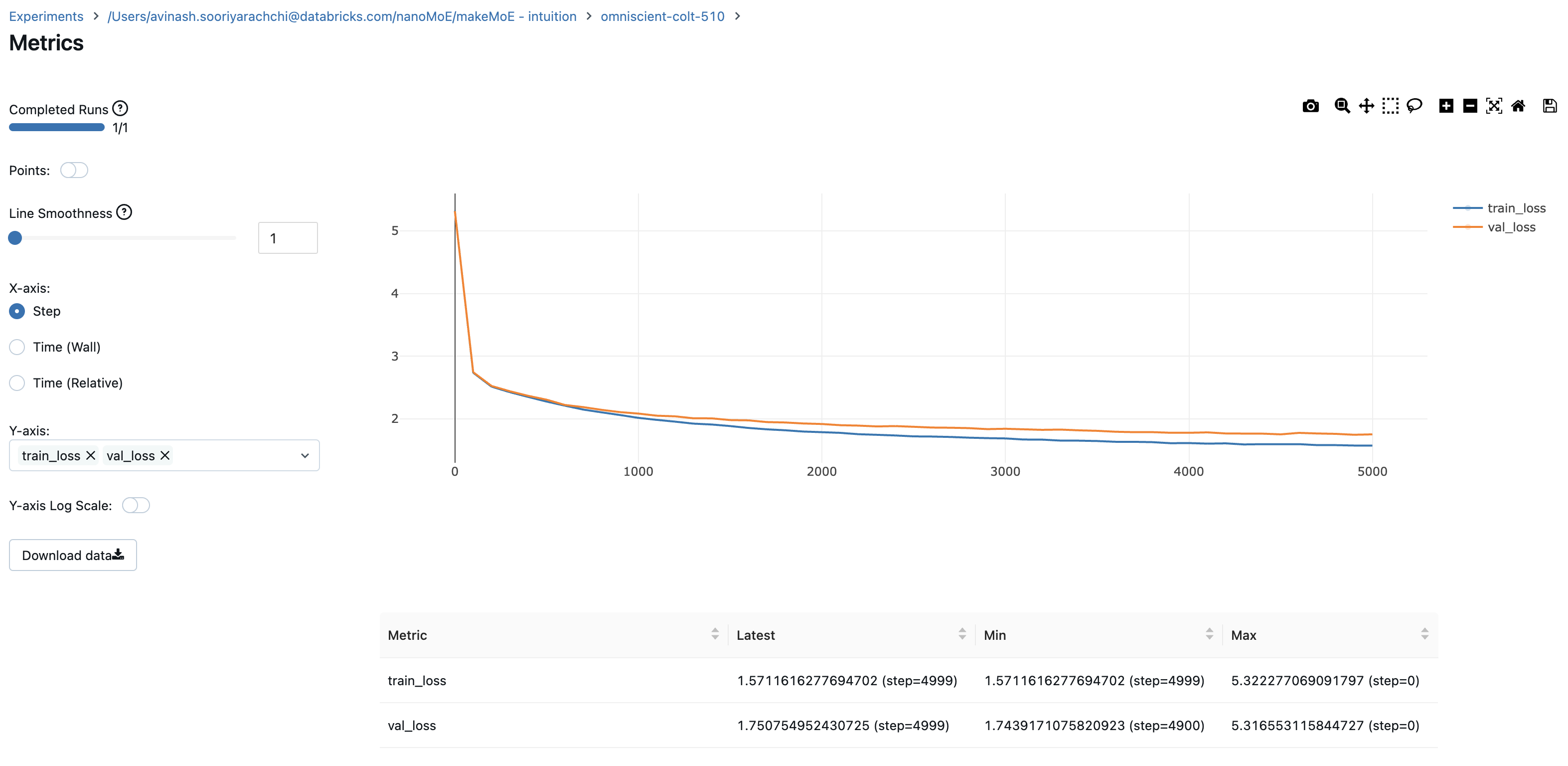
利用这个模型，我们现在可以逐个字符地生成文本，采用自回归方式进行。考虑到这是一个参数大约为 900 万的稀疏激活模型，其性能已经非常出色。

# generate from the model. Not great. Not too bad either
context = torch.zeros((1, 1), dtype=torch.long, device=device)
print(decode(m.generate(context, max_new_tokens=2000)[0].tolist()))

DUKE VINCENVENTIO:
If it ever fecond he town sue kigh now,
That thou wold'st is steen 't.

SIMNA:
Angent her; no, my a born Yorthort,
Romeoos soun and lawf to your sawe with ch a woft ttastly defy,
To declay the soul art; and meart smad.

CORPIOLLANUS:
Which I cannot shall do from by born und ot cold warrike,
What king we best anone wrave's going of heard and good
Thus playvage; you have wold the grace.
...

我希望这篇解释能帮助你更好地理解稀疏混合专家模型的架构以及它是如何一步步构建起来的。在实现这一模型的过程中，我深入参考了一系列重要的学术出版物。

专家混合模型：https://arxiv.org/pdf/2401.04088.pdf
极大型神经网络的稀疏门控专家混合层：https://arxiv.org/pdf/1701.06538.pdf

Andrej Karpathy 的原创 makemore 实现：

https://github.com/karpathy/makemore

这套代码完全是在 Databricks 上开发的，使用了一个 A100 GPU。在 Databricks 上，你可以